【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB. 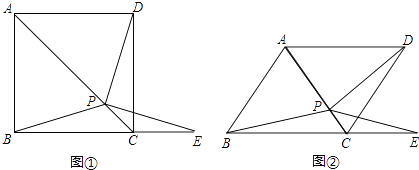
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.
参考答案:
【答案】
(1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中,
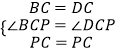 ,
,
∴△BCP≌△DCP(SAS)
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∵∠1=∠2(对顶角相等),
∴180°﹣∠1﹣∠CDP=180°﹣∠2﹣∠E,
即∠DPE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC
(3)58
【解析】(3)解:与(2)同理可得:∠DPE=∠ABC, ∵∠ABC=58°,
∴∠DPE=58°.
故答案为:58.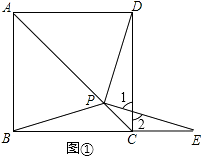
(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCP=∠DCP,然后利用“边角边”证明即可;(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;(3)根据(2)的结论解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.

(1)连接AF,CE,求证:四边形AFCE为菱形;
(2)求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明从家到图书馆看报,然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,试求:
(1)小明回家的速度.
(2)小明离家50分钟时离家的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺如图①摆放(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°).点D为AB的中点,DE交AC于点P,DF经过点C.
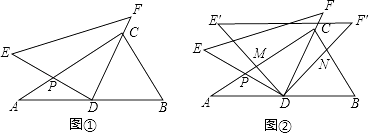
(1)求∠ADE的度数;
(2)如图②,在图①的基础上将△DEF绕点D顺时针方向旋转角α(0°<α<60°),此时的等腰直角三角尺记为△DE′F′,DE′交AC于点M,DF′交BC于点N,求证: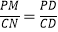 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(km)与甲出发的时间x(分)之间的关系如图所示.
(1)求甲、乙相遇时,乙所行驶的路程;
(2)当乙到达终点A时,甲还需多少分钟到达终点B?
-
科目: 来源: 题型:
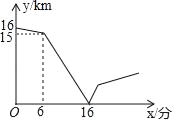
查看答案和解析>>【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为 个平方单位?
个平方单位? -
科目: 来源: 题型:
查看答案和解析>>【题目】点O在直线AB上,点A1、A2、A3,…在射线OA上,点B1、B2、B3,…在射线OB上,图中的每一个实线段和虚线段的长均为一个单位长度,一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度,按此规律,则动点M到达A101点处所需时间为____秒.

相关试题

