【题目】请将下列证明过程补充完整:已知:如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,![]() .
.
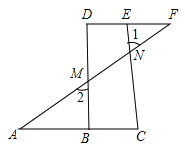
求证:![]()
证明:因为![]() (已知),
(已知),
又因为![]() ( _____________________ ),
( _____________________ ),
所以_______________(等量代换).
所以 _______ ∥______ (同位角相等,两直线平行),
所以![]() ( _____________________ ).
( _____________________ ).
又因为![]() (已知),
(已知),
所以 _______ ∥______ (_____________________ ).
所以 _______________(两直线平行,内错角相等).
所以![]() (_____________________ ).
(_____________________ ).
参考答案:
【答案】答案见解析.
【解析】
试题分析:根据对顶角相等可知∠1=∠ANC,根据同位角相等,两直线平行,可知DB∥EC,再根据平行线的性质可知∠ABD=∠C,再根据平行线的性质以及判定即可得出答案.
试题解析:∵∠1=∠2 (已知).
又∵∠1=∠ANC (对顶角相等),
∴∠2=∠ANC(等量代换).
∴DB∥EC(同位角相等,两直线平行).
∴∠ABD=∠C (两直线平行,同位角相等)
又∵∠A=∠F(已知),
∴DF∥AC(内错角相等,两直线平行),
∴∠D=∠ABD(两直线平行,内错角相等).
∴∠C=∠D(等量代换).
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某镇中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)、求饮用水和蔬菜各有多少件?
(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该镇中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G.

(1)求证:AD垂直平分EF;
(2)若∠BAC=60°,猜测DG与AG间有何数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC, ∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,
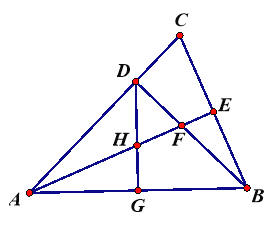
(1)求∠ACB的度数;
(2)HE=
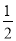 AF
AF -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将一个长为4a,宽为2b的长方形,沿图中虚线均匀分成4个小长方形,然后按图2形状拼成一个正方形。
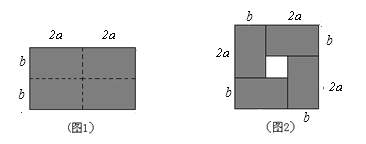
(1)图2的空白部分的边长是多少?(用含ab的式子表示)
(2)若
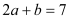 ,求图2中的空白正方形的面积。
,求图2中的空白正方形的面积。(3)观察图2,用等式表示出
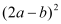 ,ab和
,ab和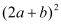 的数量关系。
的数量关系。 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数中,能作为一个三角形三边边长的是( )
A. 1,1,2 B. 1,2,4 C. 2,3,4 D. 2,4,6
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形一边上的中线把三角形分成的两个三角形的面积关系为_____.
相关试题

