【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
参考答案:
【答案】C
【解析】首先三角形的外角等于与它不相邻的两个内角的和可得∠A=∠EFB –∠E,再根据根据平行线的性质得到∠EFB=∠C.
解:∵AB∥CD,∠C=45°,
∴∠EFB=∠C=45°,
∵∠E=20°,
∴∠A=∠EFB –∠E =25°,
故选C.
“点睛”此题主要考查了平行线的性质,三角形的外角性质,关键是熟练掌握①平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等;②三角形的外角等于与它不相邻的两个内角的和,解题关键是求出∠EFB的度数,注意:两直线平行,同位角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】与点 P (a+2,-a-1)在同一个象限内的点是( )
A. (2,-1)B. (-1,2)C. (-2,-1)D. (2,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,点D是△ABC外的一点,点E在BC边的延长线上,BD平分∠ABC,CD平分∠ACE.试探究∠D与∠A的数量关系.
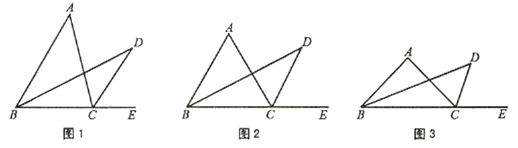
(1)特例探究:
如图2,若△ABC是等边三角形,其余条件不变,则∠D=;
如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,与∠A度数的比是 ;
(2)猜想证明:
如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示平面直角坐标系中,已知A(-2,2),B(-3,-2),C(3,-2).

(1)在图中画出△ABC;
(2)将△ABC先向上平移4个单位长,再向右平移2个单位长得到△A1B1C1,写出点A1,B1,C1的坐标;
(3)求△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,则AM平分∠DAB吗?试说明理由。(提示:过点M作ME垂直AD于E)。
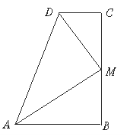
-
科目: 来源: 题型:
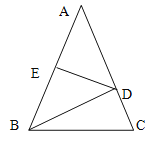
查看答案和解析>>【题目】如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,
① 若△BCD的周长为8,求BC的长;
② 若BC=4,求△BCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
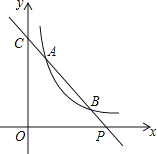
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
相关试题

