【题目】如图,已知直线y=ax+b与双曲线y=(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
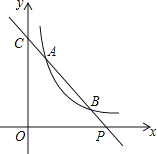
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1,x2,x0之间的关系(不要求证明).
参考答案:
【答案】(1)P(4,O);(2)A(2,2),B(4,1).(3)x1+x2=x0.
【解析】
试题分析:(1)先把A(1,3)),B(3,y2)代入y=![]() 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出![]() ,
,![]() ,根据题意得出
,根据题意得出![]() ,
,![]() ,从而求得B(
,从而求得B(![]() ,
,![]() y1),然后根据k=xy得出x1
y1),然后根据k=xy得出x1 ![]() y1=
y1=![]()
![]() y1,求得x1=2,代入
y1,求得x1=2,代入![]() ,解得y1=2,即可求得A、B的坐标;
,解得y1=2,即可求得A、B的坐标;
(3)结合(1),(2)中的结果,猜想x1+x2=x0.
试题解析:(1)∵直线y=ax+b与双曲线y=![]() (x>0)交于A(1,3),
(x>0)交于A(1,3),
∴k=1×3=3,
∴y=![]() ,
,
∵B(3,y2)在反比例函数的图象上,
∴y2=![]() =1,
=1,
∴B(3,1),
∵直线y=ax+b经过A、B两点,
∴![]() 解得
解得![]() ,
,
∴直线为y=-x+4,
令y=0,则x=4,
∴P(4,O);
(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,
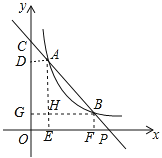
则AD∥BG∥x轴,AE∥BF∥y轴,
∴![]() ,
,![]() ,
,
∵b=y1+1,AB=BP,
∴![]() ,
,![]() ,
,
∴B(![]() ,
,![]() y1)
y1)
∵A,B两点都是反比例函数图象上的点,
∴x1y1=![]()
![]()
![]() y1,
y1,
解得x1=2,
代入![]() ,解得y1=2,
,解得y1=2,
∴A(2,2),B(4,1).
(3)根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )

A. 5° B. 15° C. 25° D. 35°
-
科目: 来源: 题型:
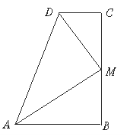
查看答案和解析>>【题目】(11分)如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,则AM平分∠DAB吗?试说明理由。(提示:过点M作ME垂直AD于E)。
-
科目: 来源: 题型:
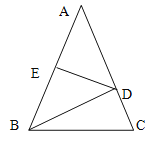
查看答案和解析>>【题目】如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,
① 若△BCD的周长为8,求BC的长;
② 若BC=4,求△BCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标平面内一点M,到x轴的距离是8,到y轴的距离是5,则点M的坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(2m+4,m﹣1)在x轴上,点P1与点P关于y轴对称,那么点P1的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”期间,某电器按成本价提高30%后标价,再打8折(标价的80%)销售,售价为2080元,设该电器的成本价为x元,根据题意,下面所列方程正确的是( )
A. x·(1+30%)×80%=2 080 B. x·30%·80%=2 080
C. 2 080×30%×80%=x D. x·30%=2 080×80%
相关试题

