【题目】如图,如图,在△ABC中,∠C=90,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为______cm.

参考答案:
【答案】15
【解析】
根据角平分线性质可得DC=DE,由题中条件可得Rt△ACD≌Rt△AED,进而得出AC=AE,通过等量代换即可求得△BDE的周长.
解:∵AD平分∠CAB,且∠C=90°,DE⊥AB,
∴DC=DE.
又∵AD=AD
∴△ACD≌△AED.
∴AC=AE.
又∵AC=BC,
∴DE+EB+BD=DC+EB+BD=BC+EB=AC+EB=AE+EB=AB.
又∵AB=15cm,
∴△DBE的周长=DB+BE+DE=15cm.
∴△DBE的周长是15cm.
故答案为:15cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图.在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中正确的有______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中
 表示小强从家出发后的时间,
表示小强从家出发后的时间, 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量 与
与 之间关系的大致图象是( )
之间关系的大致图象是( )A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分,求三角形的三边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价; 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC交BC于点G,DE⊥AB于点E,DF⊥AC的延长线于点F.

(1)说明BE=CF的理由。
(2)如果AB=m,AC=n,求AE,BE的长。(用m、n表示结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知点
 ,以O为圆心,OA为半径作
,以O为圆心,OA为半径作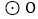 ,交y轴于点C,直线l:
,交y轴于点C,直线l: 经过点C.
经过点C. 设直线l与
设直线l与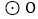 的另一个交点为
的另一个交点为 如图
如图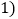 ,求弦CD的长;
,求弦CD的长; 将直线l向上平移2个单位,得直线m,如图2,求证:直线m与
将直线l向上平移2个单位,得直线m,如图2,求证:直线m与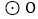 相切;
相切;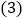 在
在 的前提下,设直线m与
的前提下,设直线m与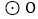 切于点P,Q为
切于点P,Q为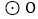 上一动点,过点P作
上一动点,过点P作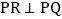 ,交直线QA于点
,交直线QA于点 如图
如图 ,则
,则 的最大面积为______.
的最大面积为______.
相关试题

