搜索
【题目】如图，两座建筑物的水平距离BC=30m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°，求这两座建筑物的高度．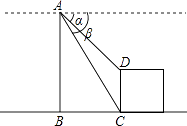
参考答案：
【答案】解：延长CD，交AE于点E，可得DE⊥AE，
在Rt△AED中，AE=BC=30m，∠EAD=30°，
∴ED=AEtan30°=10 
m，
在Rt△ABC中，∠BAC=30°，BC=30m，
∴AB=30 m，
则CD=EC﹣ED=AB﹣ED=30 ﹣10 =20 m．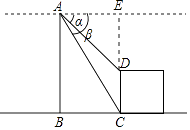
【解析】延长CD，交AE于点E，可得DE⊥AE，在直角三角形ABC中，由题意确定出AB的长，进而确定出EC的长，在直角三角形AED中，由题意求出ED的长，由EC﹣ED求出DC的长即可．
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，如果点P坐标为（m，n），向量
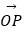可以用点P的坐标表示为 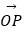=（m，n）．
已知：
=（x1 ， y1）， 
=（x2 ， y2），如果x1x2+y1y2=0，那么 与 互相垂直，下列四组向量：
①
=（2，1），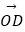 
=（﹣1，2）；
②
=（cos30°，tan45°），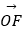 
=（1，sin60°）；
③
=（ 
﹣ 
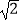，﹣2）， 
=（ + ， 
）；
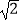④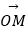
=（π0 ， 2）， 
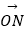=（2，﹣1）．
其中互相垂直的是（填上所有正确答案的符号）． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：|1﹣
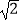|+2cos45°﹣ 
+（ 
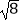）﹣1 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如下统计图表：
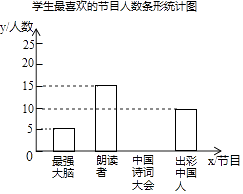
学生最喜爱的节目人数统计表节目
人数（名）
百分比
最强大脑
5
10%
朗读者
15
b%
中国诗词大会
a
40%
出彩中国人
10
20%
根据以上提供的信息，解答下列问题：
（1）x= ， a= ， b=；
（2）补全上面的条形统计图；
（3）若该校共有学生1000名，根据抽样调查结果，估计该校最喜爱《中国诗词大会》节目的学生有多少名． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E，
（1）求证：DE=DB；
（2）若∠BAC=90°，BD=4，求△ABC外接圆的半径． -
科目： 来源： 题型：
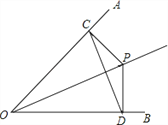
查看答案和解析>>【题目】如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D．
（1）求证：∠PCD＝∠PDC；
（2）求证：OP是线段CD的垂直平分线.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市为节约水资源，制定了新的居民用水收费标准，按照新标准，用户每月缴纳的水费y（元）与每月用水量x（m3）之间的关系如图所示．
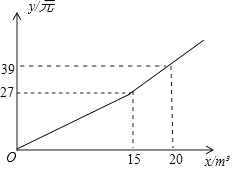
（1）求y关于x的函数解析式；
（2）若某用户二、三月份共用水40cm3（二月份用水量不超过25cm3），缴纳水费79.8元，则该用户二、三月份的用水量各是多少m3？
相关试题
