【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
参考答案:
【答案】(1) A树苗每棵300元,B种树苗每棵200元;(2) 有3种方案,其中B种树苗9棵,A种树苗21棵,最节约.
【解析】试题分析:(1)设A种树苗每棵x元,B种树苗每棵y元,根据“若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购进A种树苗m棵,则购进B种树苗(30-m)棵,根据购树费用不超过8300元结合A种树苗至少比B种树苗的2倍多2棵,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,从而得出各购树方案,再根据一次函数的性质,即可解决最值问题.
试题解析:
(1)设A种树苗每棵x元,B种树苗每棵y元,则:
![]()
解这个方程组,得: ![]()
答:A树苗每棵300元,B种树苗每棵200元。
(2)解法一:设购进A种树苗m棵,则购进B种树苗(30-m)棵,由题意,得:
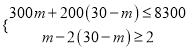
解这个不等式组,得: ![]()
又 m是整数,∴m=21、22或23
故有3种方案:A种树苗21棵,B种树苗9棵
A种树苗22棵,B种树苗8
A种树苗23棵,B种树苗7棵
由购树费用=![]() 知,m最小时最合算,
知,m最小时最合算,
∴ 方案一:A种树苗21棵,B种树苗9棵,最节约
或解法二:设购进B种树苗t棵,则有:
![]()
解得: ![]()
t是整数,∴t=7、8或9
B种树苗9棵,A种树苗21棵,最节约.
-
科目: 来源: 题型:
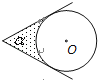
查看答案和解析>>【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A、
 B、
B、 C、
C、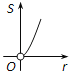 D、
D、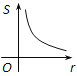
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D是AC边上一点,E是BC延长线上一点,连接DE.
(1)如图1,若点D是AC中点,且DB=DE. 求证:AD=CE.
(2)如图2,若点D是AC边上任意一点,且DB=DE,则(1)中结论是否成立,如成立,请证明;如不成立,请说明理由.

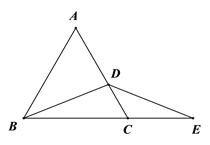
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)阅读:我们知道,
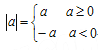 于是要解不等式
于是要解不等式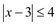 ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:解:(1)当
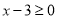 ,即
,即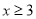 时:
时: 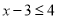
解这个不等式,得:
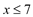
由条件
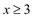 ,有:
,有: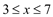
(2)当
 < 0,即 x < 3时,
< 0,即 x < 3时,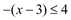
解这个不等式,得:
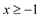
由条件x < 3,有:
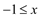 < 3
< 3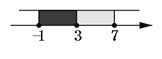
∴ 如图, 综合(1)、(2)原不等式的解为:
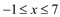
根据以上思想,请探究完成下列2个小题:
(1)
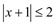 ; (2)
; (2)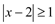 。
。 -
科目: 来源: 题型:
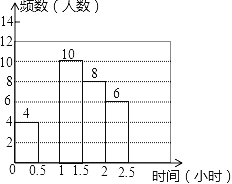
查看答案和解析>>【题目】我市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出如图所示的频数分布表和频数分布直方图的一部分.
时间/时
频数
百分比
0≤t<0.5
4
0.1
0.5≤t<1
a
0.3
1≤t<1.5
10
0.25
1.5≤t<2
8
b
2≤t<2.5
6
0.15
合计
1
(1)求表中a,b的值;
(2)补全频数分布直方图;
(3)请你估算该校1400名初中学生中,约有多少名学生在1.5小时以内完成了家庭作业.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中不一定是轴对称图形的是( )
A.长3cm的线段
B.圆
C.有60°角的三角形
D.等腰直角三角形
相关试题

