【题目】如图,△ABC是等边三角形,D是AC边上一点,E是BC延长线上一点,连接DE.
(1)如图1,若点D是AC中点,且DB=DE. 求证:AD=CE.
(2)如图2,若点D是AC边上任意一点,且DB=DE,则(1)中结论是否成立,如成立,请证明;如不成立,请说明理由.

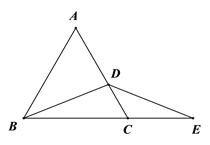
图1 图2
参考答案:
【答案】(1)证明见解析;
(2)结论成立,理由见解析.
【解析】试题分析:(1)求出∠E=∠CDE,推出CD=CE,根据等腰三角形性质求出AD=DC,即可得出答案;(2)过D作DF∥BC,交AB于F,证△BFD≌△DCE,推出DF=CE,证△ADF是等边三角形,推出AD=DF,即可得出答案.
试题解析:(1)证明:∵△ABC是等边三角形
∠ABC=∠ACB=60°
∵△ABC是等边三角形,点D为AC中点
∴BD平分∠ABC,AD =CD
∴∠DBC=![]() ∠ABC=
∠ABC=![]() ×60°=30°
×60°=30°
∵DB=DE
∴∠E=∠DBC=30°
又∵∠ACB是△DCE的外角
∴∠CDE=∠ACB-∠E=60°-30°=30°
∴∠CDE=∠E
∴CD=CE
∴CE=AD
(2) 过点D作DF∥BC交AB于F
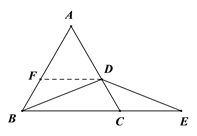
∵△ABC是等边三角形
∴∠A=∠ABC=∠ACB=60°,AB=AC
∵DF∥BC
∴∠AFD=∠ABC=60°,∠ADF=∠ACB=60°
即∠A=∠AFD=∠ADF
∴△AFD是等边三角形
∴AF=FD=AD
∴AB-AF=AC-AD
即BF=CD
∵DB=DE
∴∠E=∠DBC
∴∠ABC-∠DBC=∠ACB-∠E
即∠ABD=∠CDE
∴△FBD≌△CDE
∴CE=DF
∴CE=AD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对称轴为直线x=
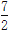 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4).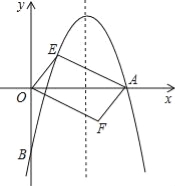
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=
 (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=
 (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
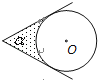
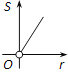
查看答案和解析>>【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A、
 B、
B、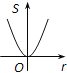 C、
C、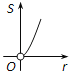 D、
D、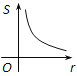
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)阅读:我们知道,
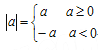 于是要解不等式
于是要解不等式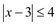 ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:解:(1)当
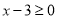 ,即
,即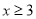 时:
时: 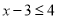
解这个不等式,得:
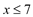
由条件
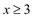 ,有:
,有: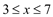
(2)当
 < 0,即 x < 3时,
< 0,即 x < 3时,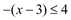
解这个不等式,得:
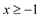
由条件x < 3,有:
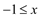 < 3
< 3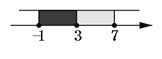
∴ 如图, 综合(1)、(2)原不等式的解为:
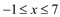
根据以上思想,请探究完成下列2个小题:
(1)
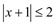 ; (2)
; (2)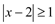 。
。
相关试题

