【题目】我市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出如图所示的频数分布表和频数分布直方图的一部分.
时间/时 | 频数 | 百分比 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)求表中a,b的值;
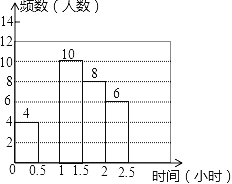
(2)补全频数分布直方图;
(3)请你估算该校1400名初中学生中,约有多少名学生在1.5小时以内完成了家庭作业.
参考答案:
【答案】(1)12 0.2
(2)图形见解析
(3)约有910名学生在1.5小时以内完成了家庭作业.
【解析】试题分析:(1)由每天完成家庭作业的时间对应的的频数和频率,如时间在1≤t<1.5的频数10和频率0.25,可求出抽查的总人数,再用总人数乘以每天完成家庭作业的时间在0.5≤t<1的频率,求出a,再用每天完成家庭作业的时间在1.5≤t<2的频数除以总人数,求出b即可;
(2)由(1)中a的值,可直接补全统计图;
(3)用每天完成家庭作业时间在1.5小时以内的频率之和乘以该校的总人数,即可得出答案.
试题解析:
(1)抽查的总的人数是:![]() =40(人),
=40(人),
a=40×0.3=12(人),
b=![]() =0.2;
=0.2;
故答案为:12,0.2;
(2)根据(1)可得:每天完成家庭作业的时间在0.5≤t<1的人数是12,补图如下:
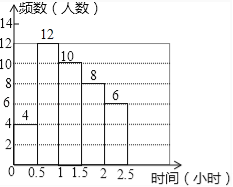
(3)根据题意得:(0.1+0.3+0.25)×1400=910(名),
答:约有910名学生在1.5小时以内完成了家庭作业.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)阅读:我们知道,
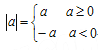 于是要解不等式
于是要解不等式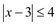 ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:解:(1)当
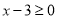 ,即
,即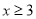 时:
时: 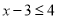
解这个不等式,得:
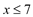
由条件
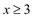 ,有:
,有: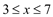
(2)当
 < 0,即 x < 3时,
< 0,即 x < 3时,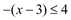
解这个不等式,得:
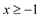
由条件x < 3,有:
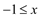 < 3
< 3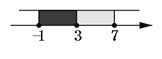
∴ 如图, 综合(1)、(2)原不等式的解为:
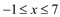
根据以上思想,请探究完成下列2个小题:
(1)
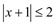 ; (2)
; (2)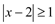 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列选项中不一定是轴对称图形的是( )
A.长3cm的线段
B.圆
C.有60°角的三角形
D.等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学足球队的18名队员的年龄情况如下表:
年龄(单位:岁)
14
15
16
17
18
人数
3
6
4
4
1
则这些队员年龄的众数和中位数分别是( )
A.15,15 B.15,15.5 C.15,16 D.16,15
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数0.397精确到0.01的结果是_____.
相关试题

