【题目】某校组织初中2000名学生游览“黄河口生态旅游区”,并以此开展“黄河文化”知识竞赛活动,现从中随机抽取若干名学生的得分![]() 满分100分,成绩均为正数
满分100分,成绩均为正数![]() 进行统计,整理出下列竞赛成绩统计表和扇形统计图
进行统计,整理出下列竞赛成绩统计表和扇形统计图![]() 均不完整
均不完整![]() .
.
成绩统计表

如果成绩在90分以上![]() 含90分
含90分![]() 可获得一等奖;70分以上
可获得一等奖;70分以上![]() 含70分
含70分![]() ,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
![]() 本次活动共随机抽取了多少名学生?
本次活动共随机抽取了多少名学生?
![]() 估计本次活动获得二等奖的学生有多少名?
估计本次活动获得二等奖的学生有多少名?
![]() 绘制频数分布直方图.
绘制频数分布直方图.
参考答案:
【答案】(1)200人;(2)1200名;()补图见解析.
【解析】
(1)由统计图表中的信息可知,成绩(x分)在![]() 这个范围内的有20人,占被抽查学生的10%,由此即可求得被抽查学生的人数;
这个范围内的有20人,占被抽查学生的10%,由此即可求得被抽查学生的人数;
(2)根据(1)中所得结果结合题中已知信息计算出成绩在![]() 范围内的学生所占的百分比,即可求出获得二等奖的学生的人数;
范围内的学生所占的百分比,即可求出获得二等奖的学生的人数;
(3)根据前面的计算结果结合已知信息计算出成绩统计表中所缺少的三个频数即可根据完整的频数分布表画出频数分布直方图.
(1)由题意可得:抽取的学生总数![]() 人
人![]() ;
;
(2)由题意可得:成绩在![]() 范围内的学生所占的百分比为:
范围内的学生所占的百分比为:![]() ,
,
∴成绩在![]() 范围内的学生所占的百分比为:
范围内的学生所占的百分比为:![]() ,
,
又∵成绩在![]() 范围内的学生所占的百分比为30%,
范围内的学生所占的百分比为30%,
∴本次活动中获得二等奖的学生约有:![]() 人
人![]() ;
;
(3)由被抽查学生总数为200人可得;
成绩在![]() 范围内的学生人数
范围内的学生人数![]() 人
人![]() ,
,
成绩在![]() 范围内的学生人数
范围内的学生人数![]() 人
人![]() ,
,
成绩在![]() 范围内的学生人数
范围内的学生人数![]() 人
人![]() ,
,
结合统计表中的已知频数画出频数分布直方图如下图所示:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.

(1)求证:∠1=∠BAD;
(2)求证:BE是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
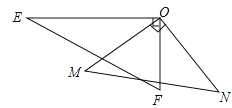
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
-
科目: 来源: 题型:
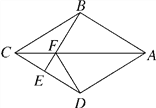
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地_____千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=
 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出方程kx+b﹣ =0的解;
=0的解;
(3)求△AOB的面积;
(4)观察图象,直接写出不等式kx+b﹣ <0的解集.
<0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,
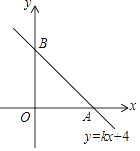
(1)求这条直线的解析式;
(2)若将这条直线沿x轴翻折,求翻折后得到的直线的解析式.
相关试题

