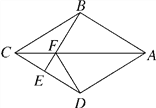
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)当BE⊥CD时,∠EFD=∠BCD
【解析】(1)利用已知条件和公共边,证得△ABC≌△ADC,即可证明∠BAC=∠DAC;再证明△ABF≌△ADF,得到∠AFB=∠AFD,再利用对顶角相等,易知结论;(2)有平行线的性质和(1)中结论,易知∠DAC=∠ACD,所以AD=CD,进而证得AB=CB=CD=AD,即可证明结论;(3)当BE⊥CD时,有(2)可知BC="CD" ,∠BCF=∠DCF,利用△BCF≌△DCF证得∠CBF=∠CDF,再利用等角的余角相等即可证明结论∠EFD =∠BCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.

(1)求证:∠1=∠BAD;
(2)求证:BE是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
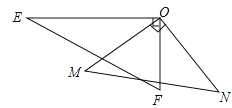
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织初中2000名学生游览“黄河口生态旅游区”,并以此开展“黄河文化”知识竞赛活动,现从中随机抽取若干名学生的得分
 满分100分,成绩均为正数
满分100分,成绩均为正数 进行统计,整理出下列竞赛成绩统计表和扇形统计图
进行统计,整理出下列竞赛成绩统计表和扇形统计图 均不完整
均不完整 .
.成绩统计表

如果成绩在90分以上
 含90分
含90分 可获得一等奖;70分以上
可获得一等奖;70分以上 含70分
含70分 ,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题: 本次活动共随机抽取了多少名学生?
本次活动共随机抽取了多少名学生? 估计本次活动获得二等奖的学生有多少名?
估计本次活动获得二等奖的学生有多少名? 绘制频数分布直方图.
绘制频数分布直方图. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A,B两地同时相向匀速行驶,当乙车到达A地后,继续保持原速向远离B的方向行驶,而甲车到达B地后立即掉头,并保持原速与乙车同向行驶,经过15小时后两车同时到达距A地300千米的C地(中途休息时间忽略不计).设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数关系如图所示,则当甲车到达B地时,乙车距A地_____千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=
 的图象的两个交点.
的图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出方程kx+b﹣ =0的解;
=0的解;
(3)求△AOB的面积;
(4)观察图象,直接写出不等式kx+b﹣ <0的解集.
<0的解集.
相关试题

