【题目】如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BAD;
(2)求证:BE是⊙O的切线.
参考答案:
【答案】
(1)
证明:∵BD=BA,
∴∠BDA=∠BAD,
∵∠1=∠BDA,
∴∠1=∠BAD;
(2)
证明:连接BO,

∵∠ABC=90°,
又∵∠BAD+∠BCD=180°,
∴∠BCO+∠BCD=180°,
∵OB=OC,
∴∠BCO=∠CBO,
∴∠CBO+∠BCD=180°,
∴OB∥DE,
∵BE⊥DE,
∴EB⊥OB,
∵OB是⊙O的半径,
∴BE是⊙O的切线.
【解析】(1)根据等腰三角形的性质和圆周角定理得出即可;(2)连接BO,求出OB∥DE,推出EB⊥OB,根据切线的判定得出即可;本题考查了三角形的外接圆与外心,等腰三角形的性质,切线的判定,熟练掌握切线的判定定理是解题的关键.
【考点精析】本题主要考查了圆周角定理和三角形的外接圆与外心的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
已知:如图1,直线AB∥CD,点E是AB、CD之间的一点,连接BE、DE得到∠BED.
求证:∠BED =∠B+∠D.
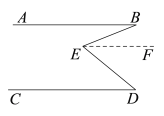 图1
图1小冰是这样做的:
证明:过点E作EF∥AB,则有∠BEF=∠B.
∵AB∥CD,∴EF∥CD.
∴∠FED=∠D.
∴∠BEF +∠FED =∠B+∠D.
即∠BED=∠B+∠D.
请利用材料中的结论,完成下面的问题:
已知:直线 AB∥CD,直线MN分别与AB、CD交于点E、F.
(1)如图2,∠BEF和∠EFD的平分线交于点G.猜想∠G的度数,并证明你的猜想;
(2)如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2.求证:∠FG1 E+∠G2=180°.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=
 ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:

(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
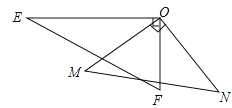
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
-
科目: 来源: 题型:
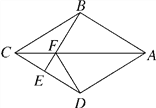
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连接DF.
(1)求证:∠BAC=∠DAC,∠AFD=∠CFE;
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织初中2000名学生游览“黄河口生态旅游区”,并以此开展“黄河文化”知识竞赛活动,现从中随机抽取若干名学生的得分
 满分100分,成绩均为正数
满分100分,成绩均为正数 进行统计,整理出下列竞赛成绩统计表和扇形统计图
进行统计,整理出下列竞赛成绩统计表和扇形统计图 均不完整
均不完整 .
.成绩统计表

如果成绩在90分以上
 含90分
含90分 可获得一等奖;70分以上
可获得一等奖;70分以上 含70分
含70分 ,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题: 本次活动共随机抽取了多少名学生?
本次活动共随机抽取了多少名学生? 估计本次活动获得二等奖的学生有多少名?
估计本次活动获得二等奖的学生有多少名? 绘制频数分布直方图.
绘制频数分布直方图.
相关试题

