Question

【题目】已知AB为⊙O的直径，C为⊙O上一点，AD与过C点的切线垂直，垂足为D，AD交⊙O于点E，∠CAB=30°

（1）如图①，求∠DAC的大小；
（2）如图②，若⊙O的半径为4，求DE的长．

Answer 1

【答案】
（1）解：连接OC，如图①，

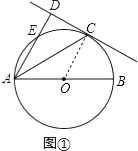
∵DC切⊙O于点C，∴OC⊥DC，又∵AD⊥DC，∴AD∥OC，∴∠DAC=∠ACO，∵OA=OC，∴∠OCA=∠CAB=30°，∴∠DAC=30°；

（2）解：连OE，OC，如图②，

∵∠EOC=2∠DAC=60°，∴△OEC为等边三角形，∴EC=OE=4，∠OCE=60°，∴∠DCE=30°，

∴DE= CE=2．

【解析】（1）：连接OC根据切线的性质定理得出OC⊥DC，又AD⊥DC，根据同一平面内垂直于同一直线的两条直线互相平行得出AD∥OC，根据平行线的性质得出∠DAC=∠ACO，根据等边对等角得出∠OCA=∠CAB=30°，利用等量代换得出结论；
（2）连OE，OC，根据同弧所对的圆心角等于圆周角的2倍得出∠EOC=2∠DAC=60°，根据有一个角为60的等腰三角形是等边三角形得出△OEC为等边三角形，根据等边三角形三边相等得出EC=OE=4，然后利用含30角的直角三角形的边角关系得出DE的长。
【考点精析】关于本题考查的平行线的判定与性质和含30度角的直角三角形，需要了解由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能得出正确答案．