Question

【题目】如图，某河堤的横断面是梯形ABCD，BC∥AD，BE⊥AD于点E，AB=50米，BC=30米，∠A=60°，∠D=30°．求AD的长度．

Answer 1

【答案】解：作CF⊥AD于点F，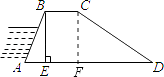

∵BE⊥AD，AB=50米，∠A=60°，

∴BE=ABsin60°=50× =25 ，

∴AE= =25，

∵BC∥AD，CF⊥AD，

∴CF=BE=25，EF=BC=30，在Rt△CFD中，∠D=30°，

∴FD=

= =75，

∴AD=AE+EF+FD=25+30+75=130（米）．

【解析】作CF⊥AD于点F，在Rt△ABE中，利用锐角三角形函数得出BE的长，再利用勾股定理得出AE的长，根据题意知四边形EFCB是矩形，根据矩形的性质得出CF=BE=25，EF=BC=30，在Rt△CFD中，∠D=30°，根据正切函数的定义得出FD的长，然后根据AD=AE+EF+FD得出答案。