【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5 cm高度处连通(即管子底离容器底5 cm),现三个容器中,只有甲中有水,水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm.
cm.
(1)开始注水1分钟,丙的水位上升________cm;
(2)开始注入________分钟的水量后,乙的水位比甲高0.5 cm.

参考答案:
【答案】 ![]()
![]() 或
或![]()
【解析】(1)根据题意可知,进入乙丙中的水的体积相等,而乙丙的底面积半径之比为2:1,结合圆柱的体积公式即可求出乙丙的水位之比,进而求解题(1);
欲求解乙的水位比甲高0.5cm,需要分甲的水位不变和乙的水位到达管子底部,(2)甲的水位上升两种情况讨论,可现设出未知数,即开始注入t分钟水后满足条件;当甲的水位不变时,需要判断丙的水位是否到达管子底部,有没有向乙溢水,根据题意可列出![]() t-1=0.5,解出t并求出此时丙中水位,若丙中水位大于5则溢出,若小于5则没有溢出;解得丙中水向乙中溢出水,而甲中水位不变根据两者之差为0.5cm即可列出一元一次方程求解即可;第二种情况,需先求出乙的水位到达管子底部的时间,进而根据甲乙两者的水位差为0.5cm的等量关系列出一元一次方程求解.
t-1=0.5,解出t并求出此时丙中水位,若丙中水位大于5则溢出,若小于5则没有溢出;解得丙中水向乙中溢出水,而甲中水位不变根据两者之差为0.5cm即可列出一元一次方程求解即可;第二种情况,需先求出乙的水位到达管子底部的时间,进而根据甲乙两者的水位差为0.5cm的等量关系列出一元一次方程求解.
(1)∵向乙和丙注入相同量的水即注入水的体积相同,而他们的底面半径之比为2:1,
根据圆柱的体积公式可知乙、丙的水位之比为:1:4.
∵当注水1分钟,乙的水位上升![]() cm,
cm,
∴注水1分钟,丙的水位上升![]() ×4=
×4=![]() cm.
cm.
(2)设开始注入t分钟的水量后,乙的水位比甲高0.5cm,有两种情况:
①当甲的水位不变时,
∵![]() t-1=0.5,
t-1=0.5,
解得t=![]() ,
,
∵![]() ×
×![]() =6>5,
=6>5,
∴此时丙容器已向甲容器溢水.
∵5÷![]() =
=![]() (分钟),
(分钟),![]() ×
×![]() =
=![]() (cm),即经过32分钟丙容器的水到达管子底部,乙的水位上升
(cm),即经过32分钟丙容器的水到达管子底部,乙的水位上升![]() cm,
cm,
∴![]() +2×
+2×![]() (t-
(t-![]() )-1=0.5,解得t=
)-1=0.5,解得t=![]() .
.
②当乙的水位到达管子底部,甲的水位上升时,
∵乙的水位到达管子底部的时间为:![]() +(5-
+(5-![]() )÷
)÷![]() ÷2=
÷2=![]() (分钟),
(分钟),
∴5-1-2×![]() (t-
(t-![]() )=0.5,
)=0.5,
解得t=![]() .
.
综上所述开始注水![]() 或
或![]() 分钟后,乙的水位比甲高0.5cm.
分钟后,乙的水位比甲高0.5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与直线y=
 x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标. -
科目: 来源: 题型:
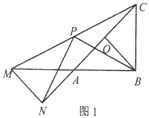
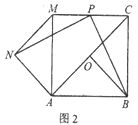
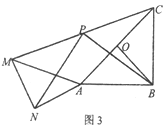
查看答案和解析>>【题目】已知,△AOB中,AB=BC=2,∠ABC=90°,点O是线段AC的中点,连接OB,将△AOB绕点A逆时针旋转α度得到△ANM,连接CM,点P是线段CM的中点,连接PN、PB.
(1)如图1,当α=180°时,直接写出线段PN和PB之间的位置关系和数量关系;
(2)如图2,当α=90°时,探究线段PN和PB之间的位置关系和数量关系,并给出完整的证明过程;
(3)如图3,直接写出当△AOB在绕点A逆时针旋转的过程中,线段PN的最大值和最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:把函数y=bx+a和函数y=ax+b(其中a,b是常数,且a≠0,b≠0)称为一对交换函数,其中一个函数是另一个函数的交换函数.比如,函数y=4x+1是函数y=x+4的交换函数,等等.
(1)直接写出函数y=2x+1的交换函数;_________________;并直接写出这对交换函数和x轴所围图形的面积为_____________________________;
(2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3,求a的值.
(3)如图,在平面直角坐标xOy中,矩形OABC中,点C(0,
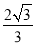 ),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数
),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数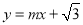 和
和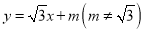 与线段EF始终都有交点,则m的取值范围为_____________________.
与线段EF始终都有交点,则m的取值范围为_____________________.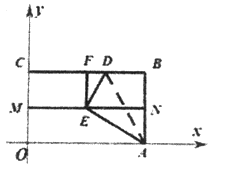
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径
 的长为( )
的长为( ) 
A.π
B.2π
C.4π
D.8π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形ABCD中,AB=12 cm,BC=6 cm.点P沿AB边从点A开始向点B以2 cm/s的速度移动;点Q沿DA边从点D开始向点A以1 cm/s的速度移动.
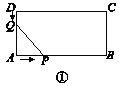
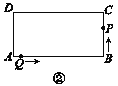
设点P,Q同时出发,用t(s)表示移动的时间.
(发现) DQ=________cm,AP=________cm.(用含t的代数式表示)
(拓展)(1)如图①,当t=________s时,线段AQ与线段AP相等?
(2)如图②,点P,Q分别到达B,A后继续运动,点P到达点C后都停止运动.
当t为何值时,AQ=
 CP?
CP?(探究)若点P,Q分别到达点B,A后继续沿着A—B—C—D—A的方向运动,当点P与点Q第一次相遇时,请直接写出相遇点的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

相关试题

