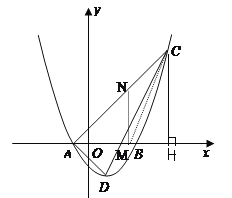
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
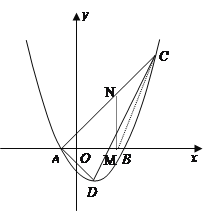
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
参考答案:
【答案】(1)![]() ;(2)M1(11-6
;(2)M1(11-6![]() ,0),M2(5,0);(3) 4
,0),M2(5,0);(3) 4![]() .
.
【解析】试题分析:(1)通过解方程即可求得OA、OB的长,从而得到点A、B的坐标,由于A、B关于抛物线的对称轴对称,且∠DAB=45°,那么△DAB是等腰直角三角形,即可利用点A、B的坐标求得点D的坐标,然后根据待定系数法求得抛物线的解析式;由于AC⊥AD,且∠DAB=45°,则∠CAB=45°,作CH⊥x轴,设出点C的纵坐标,那么其横坐标应为m-1,然后将C点坐标代入抛物线的解析式中,即可求得点C的坐标;
(2)分两种情况:①∠AMN=90°②∠ANM=90°讨论即可;
(3)易得AC、AD的长,由于△ACD是直角三角形,那么ACAD=APd1+APd2,由此可得d1+d2=![]() ,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤
,过A作AM⊥CD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤![]() ,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.
,而AC、AD、AM的长都已求得,由此可确定d1+d2的最大值.
试题解析:(1)解方程x2-4x+3=0得:x=1或x=3,而OA<OB,
则点A地坐标为(—1,0),
点B地坐标为(3,0),
∵A、B关于抛物线对称轴对称,
∴△DAB是等腰三角形,而∠DAB=45°,
∴△DAB是等腰直角三角形,得D(1,-2),
令抛物线对应的二次函数解析式为y=a(x-1)2-2,
∵抛物线过点A,
∴0=4a-2,得a=![]() ,
,
故抛物线对应的二次函数解析式为y=![]() (x-1)2-2(或写成y=
(x-1)2-2(或写成y=![]() x2-x-
x2-x-![]() ,或y=
,或y=![]() (x+1)(x—3));
(x+1)(x—3));
∵CA⊥AD,∠DAC=90°,又∵∠DAB=45°,
∴∠CAB=45°,
作CH⊥x轴,
则CH=AH,
设CH=AH=m,则OH=m-1,
∴C的坐标为(m-1,m),
代入抛物线解析式,解得:m1=6,m2=0(舍去)
故点C的坐标为(5,6);
(2)由(1)得AC=6![]() ,
,
①若∠AMN=90°,
则∠MNC=135°,
故CN=MN,设MN=n,
则MN=CN=n,AN=![]() n,
n,
则![]() n+n=6
n+n=6![]() ,n=12-6
,n=12-6![]() ,
,
∴M1(11-6![]() ,0).
,0).
②若∠ANM=90°,

则∠MNC=90°,
又MN=CN,则∠ACM=45°,∠AMC=90°,
∴AM=CM=6,
∴OM=5,
∴M2(5,0);
(3)∵AC=6![]() ,而AD=2
,而AD=2![]() ,
,
∴DC=![]() =4
=4![]() ;
;
过A作AM⊥CD,
又∵![]() AC×AD=
AC×AD=![]() DC×AM,
DC×AM,
∴AM=![]() ,
,
又∵S△ADC=S△APD+S△APC
∴![]() ×AC×AD=
×AC×AD=![]() AP×d1+
AP×d1+![]() AP×d2,
AP×d2,
d1+d2=![]()
![]() =24×
=24×![]() =4
=4![]() ;
;
即此时d1+d2的最大值为4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电视厂要印刷产品宣传材料,甲印刷厂提出:每份材料收
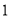 元印刷费,另收
元印刷费,另收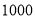 元制版费,乙厂提出:每份材料收
元制版费,乙厂提出:每份材料收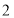 元印刷费,不收制版费.
元印刷费,不收制版费. (1)分别写出两厂的收费
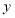 (元)与印制数量
(元)与印制数量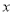 (份)之间的函数解析式;
(份)之间的函数解析式;(2)电视机厂拟拿出
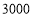 元用于印刷宣传材料,找哪家印刷厂印刷的宣传材料能多一些?
元用于印刷宣传材料,找哪家印刷厂印刷的宣传材料能多一些?(3)印刷数量在什么范围时,在甲厂印刷合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时 间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
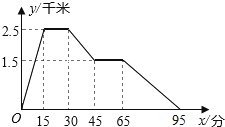
A. 体育场离张强家2.5千米
B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店1.千米
D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=1cm
(1)求AC的长
(2)若点E在直线AD上,且EA=2cm,求BE的长

-
科目: 来源: 题型:
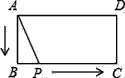
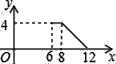
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
A.
 B.
B. 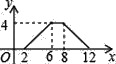 C.
C. 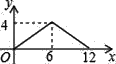 D.
D. 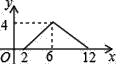
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程式应用题.
天河食品公司收购了200吨新鲜柿子,保质期15天,该公司有两种加工技术,一种是加工为普通柿饼,另一种是加工为特级霜降柿饼,也可以不需加工直接销售.相关信息见表:
品种
每天可加工数量(吨)
每吨获利(元)
新鲜柿子
不需加工
1000元
普通柿饼
16吨
5000元
特级霜降柿饼
8吨
8000元
由于生产条件的限制,两种加工方式不能同时进行,为此公司研制了两种可行方案:
方案1:尽可能多地生产为特级霜降柿饼,没来得及加工的新鲜柿子,在市场上直接销售;
方案2:先将部分新鲜柿子加工为特级霜降柿饼,再将剩余的新鲜柿子加工为普通柿饼,恰好15天完成.
请问:哪种方案获利更多?获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,欢欢和乐乐分别站在正方形
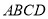 的顶点
的顶点 和顶点
和顶点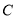 处,欢欢以
处,欢欢以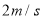 的速度走向终点
的速度走向终点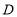 ,途中位置记为点
,途中位置记为点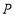 ;乐乐以
;乐乐以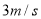 的速度走向终点
的速度走向终点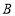 ,途中位置记为
,途中位置记为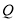 .假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为
.假设两人同时出发,两人都到达终点时结束运动.已知正方形边长为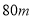 ,点
,点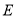 在
在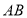 上,
上,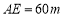 .记三角形
.记三角形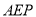 的面积为
的面积为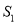 ,三角形
,三角形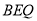 的面积为
的面积为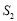 .设出发时间为
.设出发时间为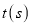 :
: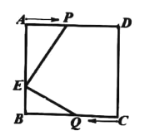
(1)如图情况,用含
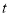 的代数式表示下列线段的长度:
的代数式表示下列线段的长度: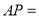 ______;
______;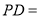 ______;
______; 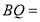 ______;
______;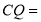 ______;
______;(2)如图情况,他们出发多少秒后
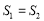 ?
?(3)是否存在这样的时刻
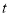 ,使得
,使得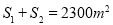 ?若存在,请求出
?若存在,请求出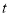 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
相关试题

