【题目】某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点。
⑴该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2,在图③中(三角板一边与OC重合),CN2=BN2+CD2,请你对这名成员在图①和图③中发现的结论选择其一说明理由。

⑵试探究图②中BN、CN、CM、DN这四条线段之间的数量关系,写出你的结论,并说明理由。

⑶将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之 间所满足的数量关系(不需要证明)
参考答案:
【答案】⑴见解析⑵CM2+CN2=DM2+BN2,理由见解析⑶CM2-CN2+ DM2-BN2=2
【解析】⑴选择图①证明:
连结DN
∵矩形ABCD
∴BO=DO ∠DCN=900
∵ON⊥BD
∴NB=ND
∵∠DCN=900
∴ND2=NC2+CD2
∴BN2=NC2+CD2 (4分)
注:若选择图③,则连结AN同理可证并类比给分
⑵CM2+CN2=DM2+BN2 理由如下:
延长DO交AB于E
∵矩形ABCD
∴BO=DO ∠ABC=∠DCB=900
AB∥CD
∴∠ABO=∠CDO ∠BEO=∠DMO
∴△BEO≌△DMO
∴OE=OM BE=DM
∵MO⊥EM
∴NE=NM
∵∠ABC=∠DCB=900
∴NE2=BE2+BN2 NM2=CN2+CM2
∴CN2+CM2 =BE2+BN2
即CN2+CM2 =DM2+BN2 (4分)
⑶CM2-CN2+ DM2-BN2=2(2分)
(1)作辅助线,连接DN,在Rt△CDN中,根据勾股定理可得:ND2=NC2+CD2,再根据ON垂直平分BD,可得:BN=DN,从而可证:BN2=NC2+CD2;
(2)作辅助线,延长MO交AB于点E,可证:△BEO≌△DMO,NE=NM,在Rt△BEN和Rt△MCN中,根据勾股定理和对应边相等,可证:CN2+CM2=DM2+BN2;
(3)根据正方形的性质知:OA=OB,∠OAM=∠OBN,∠AOB=∠AOM+∠BOM=90°,∠MON为直角三角板的直角,可知:∠MON=∠BOM+∠BON=90°,可得:∠AOM=∠BON,从而可证:△AOM≌△BON,AM=BN,又AB=BC,可得:BM=CN,在Rt△ADM和△BCM中,根据勾股定理:DM2=AM2+AD2=BN2+AD2,MC2=MB2+BC2=CN2+BC2,故可得:CM2-CN2+DM2-BN2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,AD与⊙O相切于点B,D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( )

A.70°
B.105°
C.100°
D.110° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量AD=10cm,BE=15cm, 则该自来水管的半径为( )cm.

A.5
B.10
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,
其中正确的是( )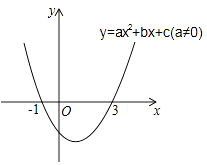
A.①②③
B.①②④
C.①④
D.②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示,若油面宽AB=600mm,则油的最大深度为mm.
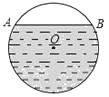
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD位于平面直角坐标系的第一象限,B、C在x轴上A点函数
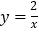 上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。
上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。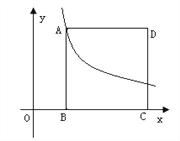
⑴试判断四边形ABCD的形状。
⑵如图若点P是线段BD上一点PE⊥BC于E,M是PD的中点,连EM、AM。
求证:AM=EM
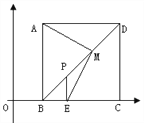
⑶在图中,连结AE交BD于N,则下列两个结论:
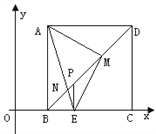
①
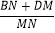 值不变;②
值不变;②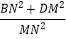 的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
相关试题

