【题目】如图,过矩形ABCD的四个顶点作对角线AC、BD的平行线,分别相交于E、F、G、H四点,则四边形EFGH为( )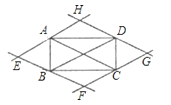
A.平行四边形
B.矩形
C.菱形
D.正方形
参考答案:
【答案】C
【解析】解:由题意知,HG∥EF∥AC,EH∥FG∥BD,HG=EF=AC,EH=FG=BD,
∴四边形EFGH是平行四边形,
∵矩形的对角线相等,
∴AC=BD,
∴EH=HG,
∴平行四边形EFGH是菱形.
故选C.
【考点精析】利用菱形的判定方法和矩形的性质对题目进行判断即可得到答案,需要熟知任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.

(1)探究猜想:
①若∠A=20°,∠D=40°,则∠AED=
②猜想图①中∠AED,∠EAB,∠EDC的关系,并用两种不同的方法证明你的结论.
(2)拓展应用:
如图②,射线FE与l1 , l2交于分别交于点E、F,AB∥CD,a,b,c,d分别是被射线FE隔开的4个区域(不含边界,其中区域a,b位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(任写出两种,可直接写答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
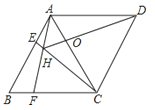
A.①②
B.①③
C.②③
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣b=2,3a+2b=3,则3a(a﹣b)+2b(a﹣b)=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,六边形ABCDEF的内角都相等,CF∥AB.
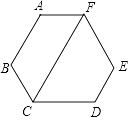
(1)求∠FCD的度数;
(2)求证:AF∥CD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+b2-8a-10b+41=0,求5a-b2+25的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:n(m﹣n)(p﹣q)﹣n(n﹣m)(p﹣q)=__.
相关试题

