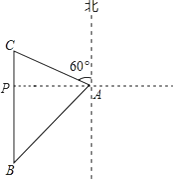
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30 ![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
参考答案:
【答案】解:过点A作AP⊥BC,垂足为P.
在Rt△APB中,∵∠APB=90°,∠PAB=45°,AB=30 ![]() ,
,
∴BP=AP= ![]() AB=30
AB=30 ![]() .
.
在Rt△APC中,∵∠APC=90°,∠PAC=30°,
∴tan∠PAC= ![]() ,
,
∴CP=APtan∠PAC=30.
∵PC+BP=BC=30+30 ![]() ,
,
∴航行时间:(30+30 ![]() )÷30=1+
)÷30=1+ ![]() (小时).
(小时).
答:该渔船从B处开始航行(1+ ![]() )小时到达C处
)小时到达C处
【解析】过点A作AP⊥BC,垂足为P,在Rt△APB利用三角函数求的AP和PB的长,则在直角△APC中利用三角函数即可求得PC的长,即可求得BC的长,然后根据速度公式求解.
-
科目: 来源: 题型:
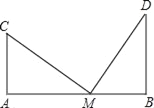
查看答案和解析>>【题目】如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
-
科目: 来源: 题型:
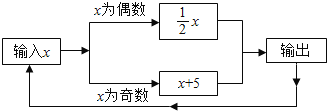
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2017次输出的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的条形统计图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
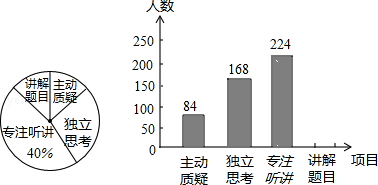
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将条形统计图补充完整;
(4)如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考”的约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某班将举行“数学知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:

请根据上面的信息,解决问题:
(1)试计算两种笔记本各买了多少本?
(2)请你解释:小明为什么不可能找回68元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
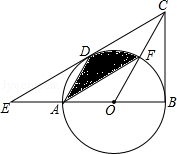
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,
 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论 ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:小青:
 ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;小夏:
 ;小雨:
;小雨: .
.这四位同学写出的结论中不正确的是



A. 小青 B. 小何 C. 小夏 D. 小雨
相关试题

