【题目】如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC= ![]() +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .
+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 . 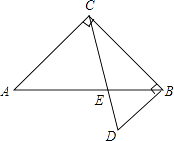
参考答案:
【答案】1
【解析】解:过点E作EH垂直BC于H。

∵∠CBD=90°,∠D=60°,
∴∠BCD=30°,
∴∠ACE=60°,
∵AC=BC= ![]() +1,
+1,
∴BD= ![]() ,AB=
,AB= ![]() (
( ![]() +1),
+1),
∵∠AEC=∠BED,
∴△BDE∽△ACE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE= ![]() ,AE=
,AE= ![]() ,
,
∵∠ACB=90°,
∴△BHE∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴EH=1,
故答案为1.
过点E作EH垂直BC于H。AC=BC=![]() ,∠D=60°,根据特殊锐角的三角函数值可以求出BD,AB的长,进而判断出△BDE∽△ACE,根据相似三角形对应边成比例得出BE,AE的长,再判断出△BHE∽△BCA,根据对应边成比例得出EH的长。
,∠D=60°,根据特殊锐角的三角函数值可以求出BD,AB的长,进而判断出△BDE∽△ACE,根据相似三角形对应边成比例得出BE,AE的长,再判断出△BHE∽△BCA,根据对应边成比例得出EH的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 中,
中, 点
点 是边
是边 上一点,点
上一点,点 分别是边
分别是边 和
和 延长线上的点,
延长线上的点,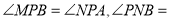
 线段
线段 的延长线和射线NF的反向延长线交于点
的延长线和射线NF的反向延长线交于点 ,若
,若
 .则
.则 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在A、B两家超市发现他看中的随身听和书包的单价都相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元.
(1)求小明看中的随身听和书包单价各是多少元?
(2)假日期间商家开展促销活动,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(购物满100元返购物券30元,购物满200元返购物券60元,以此类推;不足100元不返券,购物券可通用).小明只有400元钱,他能买到一只随身听和一个书包吗?若能,选择在哪一家购买更省钱.
-
科目: 来源: 题型:
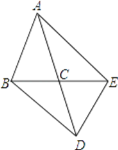
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲
乙
丙
丁
平均数/环
9.5
9.5
9.6
9.6
方差/环2
5.1
4.7
4.5
5.1
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理填空:
如图,
 分别在
分别在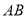 和
和 上,
上,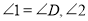 与
与 互余,
互余, 于
于 求证:
求证:

证明:
 (已知)
(已知) ( )
( ) (已知)
(已知)
 ( )
( ) ( )
( )又
 (已知)
(已知) ( )
( )

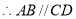 ( ).
( ).
相关试题

