Question

【题目】如图，已知抛物线y=（x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．

（1）求点A、B、C的坐标；

（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；

（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）点C（0，﹣）　　（2）﹣　　（3）（﹣4，2）或（6，2）或（0，﹣）

【解析】（1）令y=0可求得点A、点B的横坐标，令x=0可求得点C的纵坐标；

（2）根据两点之间线段最短作M点关于直线x=﹣2的对称点M′，当N（﹣2，N）在直线M′B上时，MN+BN的值最小；

（3）需要分类讨论：△PAB∽△ABD、△PAB∽△ABD，根据相似三角形的性质求得PB的长度，然后可求得点P的坐标．

解：（1）令y=0得x1=﹣2，x2=4，

∴点A（﹣2，0）、B（4，0）

令x=0得y=﹣，

∴点C（0，﹣）

（2）将x=1代入抛物线的解析式得y=﹣

∴点M的坐标为（1，﹣）

∴点M关于直线x=﹣2的对称点M′的坐标为（﹣5，）

设直线M′B的解析式为y=kx+b

将点M′、B的坐标代入得：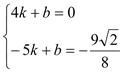

解得：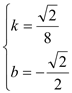

所以直线M′B的解析式为y=×．

将x=﹣2代入得：y=﹣，

所以n=﹣．

（3）过点D作DE⊥BA，垂足为E．

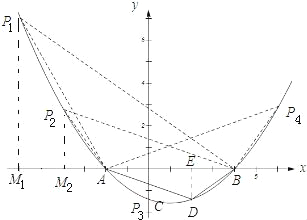
由勾股定理得：

AD===3，

BD===，

如下图，①当P1AB∽△ADB时，

=即：=，

∴P1B=6

过点P1作P1M1⊥AB，垂足为M1．

∴=即：=

解得：P1M1=6，

∵=即：=

解得：BM1=12

∴点P1的坐标为（﹣8，6）

∵点P1不在抛物线上，所以此种情况不存在；

②当△P2AB∽△BDA时，=即：=

∴P2B=6，

过点P2作P2M2⊥AB，垂足为M2．

∴=，即：=

∴P2M2=2，

∵=，即：=

∴M2B=8

∴点P2的坐标为（﹣4，2）

将x=﹣4代入抛物线的解析式得：y=2，

∴点P2在抛物线上．

由抛物线的对称性可知：点P2与点P4关于直线x=1对称，

∴P4的坐标为（6，2），

当点P3位于点C处时，两三角形全等，所以点P3的坐标为（0，﹣），

综上所述点P的坐标为：（﹣4，2）或（6，2）或（0，﹣）时，以P、A、B为顶点的三角形与△ABD相似．

“点睛”本题综合考查了二次函数、一次函数、轴对称…路径最短、相似三角形的性质，难度较大，利用相似三角形的性质求得PB的长是解题的关键，解答本题需要注意的是在不确定相似三角形的对应角和对应边的情况下分类讨论，不要漏解.