【题目】已知:a、b为有理数,下列说法:①若 a、b互为相反数,则![]() ;②若
;②若![]() 则
则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() 是正数.其中正确的有
是正数.其中正确的有
A.1个B.2个C.3个D.4个
参考答案:
【答案】B
【解析】
①0的相反数为0,而![]() 没有意义;
没有意义;
②由两数之和小于0,两数之积大于0,得到a与b都为负数,即3a+4b小于0,利用负数的绝对值等于它的相反数化简得到结果,即可作出判断;
③由ab的绝对值等于它的相反数,得到ab为非正数,得到a与b的大小,即可作出判断;
④由a绝对值大于b绝对值,分情况讨论,即可作出判断.
①0与0互为相反数,但是![]() 没有意义,本选项错误;
没有意义,本选项错误;
②由a+b<0,ab>0,得到a与b同时为负数,即3a+4b<0,
∴|3a+4b|=3a4b,本选项正确;
③∵|ab|+ab=0,即|ab|=(ab),
∴ab≤0,即a≤b,本选项错误;
④若|a|>|b|,
当a>0,b>0时,可得a>b,即ab>0,a+b>0,∴(a+b)(ab)为正数;
当a>0,b<0时,ab>0,a+b>0,∴(a+b)(ab)为正数;
当a<0,b>0时,ab<0,a+b<0,∴(a+b)(ab)为正数;
当a<0,b<0时,ab<0,a+b<0,∴(a+b)(ab)为正数,
本选项正确,
则其中正确的有2个.
故选:B.
【点晴】
此题考查了有理数的混合运算,熟练掌握各种运算法则是解本题的关键.
-
科目: 来源: 题型:
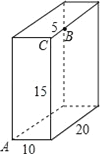
查看答案和解析>>【题目】长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个长为
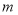 ,宽为
,宽为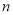 的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.
的长方形内,该长方形内部未被卡片覆盖的部分用阴影表示.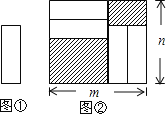
(1)能否用只含
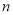 的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含
的式子表示出图②中两块阴影部分的周长和?_____(填“能”或“不能”);(2)若能,请你用只含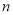 的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____.
的式子表示出中两块阴影部分的周长和;若不能,请说明理由_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=
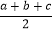 ,那么这个三角形的面积S=
,那么这个三角形的面积S=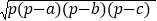 .这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:
.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式。中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦---九韶公式”完成下列问题:如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1 +h2的值
相关试题

