【题目】如图,在平面直角坐标系xOy中,直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),并与y= ![]() 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线.
(1)求一次函数与反比例函数的解析式;
(2)若点C′是点C关于y轴的对称点,请求出△ABC′的面积.
参考答案:
【答案】
(1)
解:∵直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),
∴ ![]() ,
,
解得 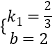 .
.
∴一次函数的解析式为y= ![]() x+2.
x+2.
∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4.
∴C(3,4).
∵点C在双曲线y= ![]() 上,
上,
∴k2=3×4=12.
∴反比例函数的解析式为y= ![]() .
.
(2)
解:∵点C′是点C(3,4)关于y轴的对称点,
∴C′(﹣3,4).
∴AC′⊥AO.
∴S△ABC′=S梯形AOBC′﹣S△ABO= ![]() (2+4)×3﹣
(2+4)×3﹣ ![]() 3×2=6.
3×2=6.
【解析】(1)根据直线y=k1x+b交x轴于点A(﹣3,0),交y轴于点B(0,2),代入解析式,求出k1和b的值,从而得出一次函数的解析式;再根据OB是△ACD的中位线,得出点C的坐标,最后代入双曲线y= ![]() ,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.
,即可求出反比例函数的解析式.(2)根据点C′是点C(3,4)关于y轴的对称点,求出C′的坐标,从而得出AC′⊥AO,最后根据S△ABC′=S梯形AOBC′﹣S△ABO , 代入计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(3﹣π)0+2sin60°+(
 )﹣2﹣|﹣
)﹣2﹣|﹣ 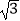 |
| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F.

(1)求证:△ABF∽△ECF;
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】“中秋节”是我国的传统佳节,历来都有赏月,吃月饼的习俗.小明家吃过晚饭后,小明的母亲在桌子上放了四个包装纸盒完全一样的月饼,它们分别是2个豆沙,1个莲蓉和1个叉烧.
(1)小明随机拿一个月饼,是莲蓉的概率是多少?
(2)小明随机拿2个月饼,请用树形图或列表的方法表示所有可能的结果,并计算出没有拿到豆沙月饼的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应区“美丽广西 清洁乡村”的号召,某校开展“美丽广西 清洁校园”的活动,该校经过精心设计,计算出需要绿化的面积为498m2 , 绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍.结果一共用20天完成了该项绿化工作.
(1)该项绿化工作原计划每天完成多少m2?,
(2)在绿化工作中有一块面积为170m2的矩形场地,矩形的长比宽的2倍少3m,请问这块矩形场地的长和宽各是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.
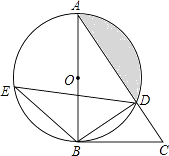
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)在(1)的条件下,若tanE=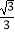 ,BC=
,BC= 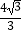 ,求阴影部分的面积.(计算结果精确到0.1)
,求阴影部分的面积.(计算结果精确到0.1)
(参考数值:π≈3.14,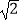 ≈1.41,
≈1.41, 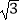 ≈1.73)
≈1.73) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2 . C2的图象与x轴交于A、B两点(点A在点B的左侧).
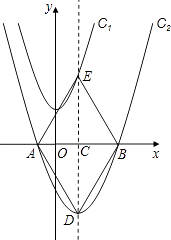
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.
相关试题

