【题目】小明在研究数学问题时遇到一个定义:将三个已经排好顺序的数:![]() ,
,![]() ,
,![]() ,称为数列
,称为数列![]() ,
,![]() ,
,![]() .计算
.计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列
,将这三个数的最小值称为数列![]() ,
,![]() ,
,![]() 的最佳值.例如,对于数列2,
的最佳值.例如,对于数列2,![]() ,3,因为
,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,
,所以数列2,![]() ,3的最佳值为
,3的最佳值为![]() .
.
小明进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列![]() ,2,3的最佳值为
,2,3的最佳值为![]() ;数列3,
;数列3,![]() ,2的最佳值为1;
,2的最佳值为1;![]() .经过研究,小明发现,对于“2,
.经过研究,小明发现,对于“2,![]() ,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)求数列![]() ,
,![]() ,2的最佳值;
,2的最佳值;
(2)将“![]() ,
,![]() ,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
,1”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将3,![]() ,
,![]() 这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求
这三个数按照不同的顺序排列,可得到若干个数列.若使数列的最佳值为1,求![]() 的值.
的值.
参考答案:
【答案】(1)0;(2)1;-3,1,-6或1,-3,-6.;(3)a=8或12或4或10
【解析】
(1)根据上述材料给出的方法计算相应的最佳值即可;
(2)要使数列的最佳值最小,就要使前两个数的和的绝对值最小,最小只能为![]() ,由此可以得出答案;
,由此可以得出答案;
(3)分情况建立方程,求得a的数值即可.
(1)解:因为![]() ,
,![]() ,
,![]() ,所以数列
,所以数列![]() ,
,![]() ,2的最佳值为0.
,2的最佳值为0.
(2)要使数列的最佳值最小,就要使前两个数的和的绝对值最小,最小只能为![]() ,
,
数列的最佳值的最小值为:![]() ,数列可以为:-3,1,-6或1,-3,-6.
,数列可以为:-3,1,-6或1,-3,-6.
故答案为:1;-3,1,-6或1,-3,-6.
(3)当![]() 时,则
时,则![]() 或
或![]() ,不符合题意;
,不符合题意;
当![]() 时,则
时,则![]() 或
或![]() ,
,
当![]() 时,则
时,则![]() 或
或![]() ,
,
所以a=8或12或4或10
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与合并同类项:
(1)+4.7+(﹣4)﹣2.7﹣(﹣3.5)
(2)11÷(﹣22)﹣3×(﹣11)
(3)16+(﹣2)3+|﹣7|+(
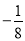 )×(﹣4)
)×(﹣4)(4)0.25×(﹣2)2﹣[﹣4÷(
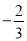 )2+1]÷(﹣1)2020
)2+1]÷(﹣1)2020(5)5x4+3x2y﹣10﹣3x2y+x4﹣1
(6)(7y﹣3z)﹣(8y﹣5z)
(7)2(2a2+9b)+3(﹣5a2﹣6b)
(8)﹣3(2x2﹣xy)﹣4(x2﹣xy﹣6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).如图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:

(1)这次活动一共调查了______名学生;
(2)在扇形统计图中,“其他“所在扇形的圆心角等于______度;
(3)补全条形统计图;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在□ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为每秒13个单位长度,沿A-D-A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度. P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A-D-A运动时,求AP的长(用含t的代数式表示).
(2) 当点P与点D重合时,求t的值
(3)连结AQ,在点P沿B-A-D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称
甲
乙
进价
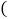 元
元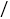 件
件
40
90
售价
 元
元 件
件
60
120
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
 写出y关于x的函数关系式:
写出y关于x的函数关系式: 该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?
该商品计划最多投入8000元用于购买者两种商品,则至少要购进多少件甲商品?若销售完这些商品,则商场可获得的最大利润是多少元?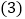 实际进货时,生产厂家对甲种商品的出厂价下调a元
实际进货时,生产厂家对甲种商品的出厂价下调a元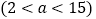 出售
出售 且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及
且限定商场最多购购进甲种商品60件,若商场保持同种商品的售价不变,请你根据以上信息及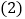 中条件,设计出使该商场获得最大利润的进货方案.
中条件,设计出使该商场获得最大利润的进货方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级开展演讲比赛,学校决定购买一些笔记本和钢笔作为奖品.现有甲、乙两家商店出售两种同样的笔记本和钢笔.他们的定价相同:笔记本定价为每本25元,钢笔每支定价6元,但是他们的优惠方案不同,甲店每买一本笔记本赠一支钢笔;乙店全部按定价的9折优惠.已知七年级需笔记本20本,钢笔x支(大于20支).问:
(1)在甲店购买需付款 元,在乙店购买需付款 元;
(2)若x=30,通过计算说明此时到哪家商店购买较为合算?
(3)当x=40时,请设计一种方案,使购买最省钱?算出此时需要付款多少元?
相关试题

