搜索
【题目】计算与合并同类项：
(1)+4.7+(﹣4)﹣2.7﹣(﹣3.5)
(2)11÷(﹣22)﹣3×(﹣11)
(3)16+(﹣2)3+|﹣7|+(
)×(﹣4)
(4)0.25×(﹣2)2﹣[﹣4÷(
)2+1]÷(﹣1)2020
(5)5x4+3x2y﹣10﹣3x2y+x4﹣1
(6)(7y﹣3z)﹣(8y﹣5z)
(7)2(2a2+9b)+3(﹣5a2﹣6b)
(8)﹣3(2x2﹣xy)﹣4(x2﹣xy﹣6)
参考答案：
【答案】(1)1.5；(2)32
；(3)15；(4)9；(5)6x4﹣11；(6)﹣y+2z；(7)﹣11a2；(8)﹣10x2+7xy+24.
【解析】
(1)直接利用有理数的加减运算法则计算得出答案；
(2)直接利用有理数的乘除运算法则计算得出答案；
(3)直接利用有理数的混合运算法则计算得出答案；
(4)直接利用有理数的混合运算法则计算得出答案；
(5)直接合并同类项得出答案；
(6)直接去括号进而合并同类项得出答案；
(7)直接去括号进而合并同类项得出答案；
(8)直接去括号进而合并同类项得出答案.
(1)+4.7+(﹣4)﹣2.7﹣(﹣3.5)
＝(4.7﹣2.7)+(﹣4+3.5)
＝2﹣0.5
＝1.5；
(2)11÷(﹣22)﹣3×(﹣11)
＝﹣+33
＝32；
(3)16+(﹣2)3+|﹣7|+(
)×(﹣4)
＝16﹣8+7+
＝15；
(4)0.25×(﹣2)2﹣[﹣4÷(
)2+1]÷(﹣1)2020
＝1﹣(﹣9+1)
＝1+8
＝9；
(5)5x4+3x2y﹣10﹣3x2y+x4﹣1
＝(5x4+x4)+(3x2y﹣3x2y)+(﹣10﹣1)
＝6x4﹣11；
(6)(7y﹣3z)﹣(8y﹣5z)
＝7y﹣3z﹣8y+5z
＝﹣y+2z；
(7)2(2a2+9b)+3(﹣5a2﹣6b)
＝4a2+18b﹣15a2﹣18b
＝﹣11a2；
(8)﹣3(2x2﹣xy)﹣4(x2﹣xy﹣6)
＝﹣6x2+3xy﹣4x2+4xy+24
＝﹣10x2+7xy+24.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，对角线AC、BD相交于点O，AB⊥AC，AB＝3cm，BC＝5cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连结PO并延长交BC于点Q，设运动时间为t(0＜t＜5)．
(1)当t为何值时，四边形ABQP是平行四边形？
(2)设四边形OQCD的面积为y(cm2)，求y与t之间的函数关系式；
(3)是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．
备用图 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，A、E、F、C在一条直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC，若AB=CD．
（1）图①中有 对全等三角形，并把它们写出来 ；
（2）求证：BG=DG，AG=CG；
（3）若将△ABF的边AF沿GA方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立，如果成立，请予证明．
-
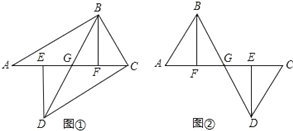
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB＝10，AC＝2
，BC边上的高AD＝6，则另一边BC等于_______．【答案】10或6
【解析】试题解析：根据题意画出图形，如图所示，
如图1所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
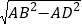=8，CD=
=2，此时BC=BD+CD=8+2=10；
如图2所示，AB=10，AC=2
，AD=6，在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
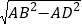=8，CD==2，此时BC=BD-CD=8-2=6，
则BC的长为6或10．
【题型】填空题
【结束】
12【题目】在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为了了解本校七年级学生课外阅读的喜好，随机抽取该校七年级部分学生进行问卷调査（每人只选一种书籍）.如图是整理数据后绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：
（1）这次活动一共调查了______名学生；
（2）在扇形统计图中，“其他“所在扇形的圆心角等于______度；
（3）补全条形统计图；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在□ABCD中，AB＝13，BC＝50，BC边上的高为12．点P从点B出发，沿B-A-D-A运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度. P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．
（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．
（2） 当点P与点D重合时，求t的值
（3）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在研究数学问题时遇到一个定义：将三个已经排好顺序的数：
，
，
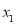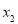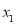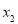，称为数列，，．计算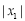
，
，
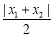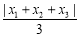，将这三个数的最小值称为数列，，的最佳值．例如，对于数列2，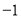
，3，因为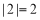
，
，
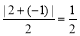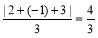，所以数列2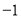，，3的最佳值为
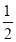．小明进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的最佳值．如数列
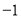，2，3的最佳值为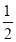；数列3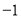，，2的最佳值为1；
．经过研究，小明发现，对于“2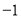，，3”这三个数，按照不同的排列顺序得到的不同数列中，最佳值的最小值为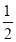．根据以上材料，回答下列问题：（1）求数列
，
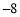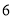，2的最佳值；（2）将“
，
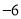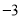，1”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的最佳值的最小值为 ，取得最佳值最小值的数列为 （写出一个即可）；（3）将3，
，
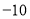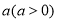这三个数按照不同的顺序排列，可得到若干个数列．若使数列的最佳值为1，求
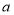的值．
相关试题
