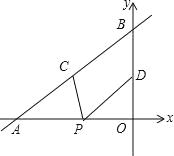
【题目】如图,直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0) B.(﹣6,0) C.(﹣![]() ,0) D.(﹣
,0) D.(﹣![]() ,0)
,0)
参考答案:
【答案】C.
【解析】
试题分析:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
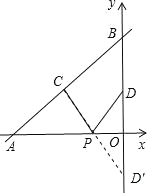
直线y=![]() x+4与x轴、y轴的交点坐标为A(﹣6,0)和点B(0,4),因点C、D分别为线段AB、OB的中点,可得点C(﹣3,2),点D(0,2).再由点D′和点D关于x轴对称,可知点D′的坐标为(0,﹣2).设直线CD′的解析式为y=kx+b,直线CD′过点C(﹣3,2),D′(0,﹣2),所以
x+4与x轴、y轴的交点坐标为A(﹣6,0)和点B(0,4),因点C、D分别为线段AB、OB的中点,可得点C(﹣3,2),点D(0,2).再由点D′和点D关于x轴对称,可知点D′的坐标为(0,﹣2).设直线CD′的解析式为y=kx+b,直线CD′过点C(﹣3,2),D′(0,﹣2),所以![]() ,解得:
,解得: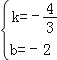 ,即可得直线CD′的解析式为y=﹣
,即可得直线CD′的解析式为y=﹣![]() x﹣2.令y=﹣
x﹣2.令y=﹣![]() x﹣2中y=0,则0=﹣
x﹣2中y=0,则0=﹣![]() x﹣2,解得:x=﹣
x﹣2,解得:x=﹣![]() ,所以点P的坐标为(﹣
,所以点P的坐标为(﹣![]() ,0).故答案选C.
,0).故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A. 必然事件发生的概率为1 B. 不可能事件发生的概率为0
C. 随机事件发生的概率大于等于0、小于等于1 D. 概率很小的事件不可能发生
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A. AB∥DC,AD=BC B. AB∥DC,AD∥BC C. AB=DC,AD=BC D. OA=OC,OB=OD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AD=4,∠AOD=60°,求AB的长.

-
科目: 来源: 题型:
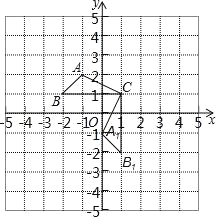
查看答案和解析>>【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=
 OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF= OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=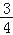 ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于多项式26﹣3x5+x4+x3+x2+x的说法正确的是( )
A. 是六次六项式 B. 是五次六项式
C. 是六次五项式 D. 是五次五项式
相关试题

