搜索
【题目】关于多项式26﹣3x5+x4+x3+x2+x的说法正确的是（ ）
A. 是六次六项式 B. 是五次六项式
C. 是六次五项式 D. 是五次五项式
参考答案：
【答案】B
【解析】
根据多项式次数的定义知，该多项式的次数是5次，又因为次多项式有6个单项式组成，所以是五次六项式．
多项式26﹣3x5+x4+x3+x2+x次数最高的项的次数是5，且有6个单项式组成，所以是五次六项式．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=
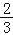x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（ ）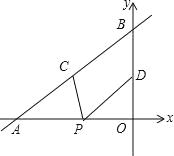
A．（﹣3，0） B．（﹣6，0） C．（﹣
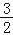，0） D．（﹣
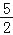，0） -
科目： 来源： 题型：
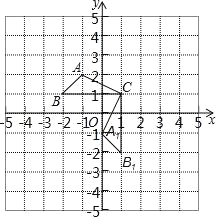
查看答案和解析>>【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（﹣1，2）、B（﹣2，1）、C（1，1）（正方形网格中每个小正方形的边长是1个单位长度）．
（1）△A1B1C1是△ABC绕点 逆时针旋转 度得到的，B1的坐标是 ；
（2）求出线段AC旋转过程中所扫过的面积（结果保留π）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是 ．
（1）EF=
OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）BE+BF=OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=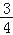
；（5）OGBD=AE2+CF2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一个直角三角形纸片ACB，其中∠ACB=90°，AC=4，BC=3，E、F分别是AC、AB边上点，连接EF．
（1）图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF=3S△EDF，求AE的长；
（2）如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M处，且使MF∥CA．
①试判断四边形AEMF的形状，并证明你的结论；
②求EF的长；
（3）如图③，若FE的延长线与BC的延长线交于点N，CN=1，CE=
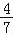，求
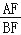的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在﹣（﹣1）4，23，﹣32，（﹣4）2这四个数中，最大的数与最小的数的和等于（ ）
A. 7 B. 15 C. ﹣24 D. ﹣1
-
科目： 来源： 题型：
查看答案和解析>>【题目】在弹性限度内，弹簧伸长的长度与所挂物体的质量呈正比，某弹簧不挂物体时长15cm，当所挂物体质量为3kg时，弹簧长16．8cm．写出弹簧长度L（cm）与所挂物体质量x（kg）之间的函数表达式 ．
相关试题
