【题目】已知点![]() 是直线
是直线![]() 上的一点,
上的一点,![]() ,射线
,射线![]() 是
是![]() 的一条三等分线,且
的一条三等分线,且![]() .(本题所涉及的角指小于平角的角)
.(本题所涉及的角指小于平角的角)
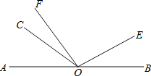
(1)如图,当射线![]() 、
、![]() 、
、![]() 在直线
在直线![]() 的同侧,
的同侧,![]() ,则
,则![]() 的度数为________;
的度数为________;
(2)如图,当射线![]() 、
、![]() 、
、![]() 在直线
在直线![]() 的同侧,
的同侧,![]() 比
比![]() 的余角大
的余角大![]() ,求
,求![]() 的度数________;
的度数________;
(3)当射线![]() 、
、![]() 在直线
在直线![]() 上方,射线
上方,射线![]() 在直线
在直线![]() 下方,
下方,![]() 小于
小于![]() ,其余条件不变,请同学们自己画出符合题意的图形,探究
,其余条件不变,请同学们自己画出符合题意的图形,探究![]() 与
与![]() 确定的数量关系式,请给出你的结论,并说明理由.
确定的数量关系式,请给出你的结论,并说明理由.
参考答案:
【答案】(1)10°;(2)20°;(3)见解析.
【解析】
(1)由∠BOE=15°,∠COE=120°,求出∠AOE的度数和∠AOC的度数,然后由∠AOF=![]() ∠AOE,求出∠AOF的度数,最后根据角的和差即可求∠COF的度数;
∠AOE,求出∠AOF的度数,最后根据角的和差即可求∠COF的度数;
(2)设∠BOE=x,则∠FOE=130°-x,由∠COE=120°,则∠AOC=60°-x,∠COF=x-10°,进而可求∠AOF=50°,然后由∠AOF=![]() ∠AOE,可求∠AOE的度数,进而可求∠BOE的度数,即x的值,从而可求∠COF的度数;
∠AOE,可求∠AOE的度数,进而可求∠BOE的度数,即x的值,从而可求∠COF的度数;
(3)∠FOC=![]() ∠BOE,画出图形,设∠AOF=x,根据∠AOF=∠AOE,∠COE=120°及角的和差,用含x的式子表示出∠FOC和∠BOE的度数,然后相比即可得到∠FOC=
∠BOE,画出图形,设∠AOF=x,根据∠AOF=∠AOE,∠COE=120°及角的和差,用含x的式子表示出∠FOC和∠BOE的度数,然后相比即可得到∠FOC=![]() ∠BOE.
∠BOE.
(1)![]() ;
;![]() 设
设![]() ,则
,则![]() 的余角为
的余角为![]() ,
,
∵![]() 比
比![]() 的余角大
的余角大![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(3)![]() ,如图所示,
,如图所示,

设![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),若一次函数的图象过A,B两点,求该一次函数的特征数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:①
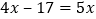 ;②
;②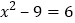 ;③
;③ ;④
;④ ;⑤
;⑤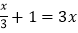 ;⑥
;⑥ ;⑦
;⑦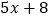 ;⑧
;⑧ 中方程有________,一元一次方程有________(只填序号).
中方程有________,一元一次方程有________(只填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】移动公司推出两种话费套餐,套餐一:每月收取月租34元后,送50分钟的通话时间,超过50分钟的部分每分钟收费0.2元,并约定每月最低消费40元(当月通话费用不足40元,一律按40元收取);套餐二:每月没有最低消费,但每分钟均收取0.4元的通话费用.若分别用y1,y2(单位:元)表示套餐一、套餐二的通话费用,用x(单位:分钟)表示每个月的通话时间.
(1)分别求出y1,y2关于x的函数表达式;
(2)在如图所示的平面直角坐标系中,画出这两个函数的图象,并直接写出这两个函数图象的交点坐标;
(3)①结合图象,如何选择话费套餐才可使每月支付的通话费用较少?
②若小亮的爸爸这个月的通话费用是64元,求使用两种套餐的通话时间相差多少分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( )
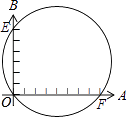
A.25个单位长度
B.14个单位长度
C.12个单位长度
D.10个单位长度 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两站相距240千米,从甲站开出一列慢车,速度为每小时80千米,从乙站开出一列快车,速度为每小时120千米.
(1)若两车同时开出,背向而行,则经过多长时间两车相距540千米?
(2)若两车同时开出,同向而行(快车在后),则经过多长时间快车可追上慢车?
(3)若两车同时开出,同向而行(慢车在后),则经过多长时间两车相距300千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A城出发沿相同的路线匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示,则下列结论:①A、B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=
 或
或 .其中正确的是________(填序号).
.其中正确的是________(填序号).
相关试题

