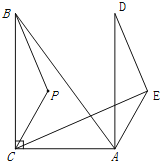
【题目】如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、
A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,
AB=6时,根据此图求PA+PB+PC的最小值.

参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】(1)①连接PB、PC,将△BCP沿射线CA方向平移,得到△DAE,点B、C、P的对应点分别为点D、A、E,连接CE,据此画图即可;②连接BD、CD,构造矩形ACBD和Rt△CDE,根据矩形的对角线相等以及勾股定理进行计算,即可求得CE的长;
(2)以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN,根据△PAM、△ABN都是等边三角形,可得PA+PB+PC=CP+PM+MN,最后根据当C、P、M、N四点共射线,PA+PB+PC的值最小,此时△CBN是直角三角形,利用勾股定理即可解决问题.
解:(1)①补全图形如图所示;
②如图,连接BD、CD
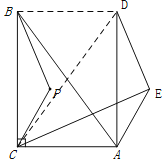
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,∴CD=AB=6,
∵BP=3,∴DE=BP=3,
∵BP⊥CE,BP∥DE,∴DE⊥CE,
∴在Rt△DCE中, ![]() ;
;
(2)证明:如图所示,
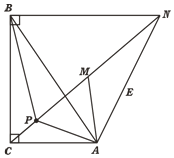
当C、P、M、N四点共线时,PA+PB+PC最小
由旋转可得,△AMN≌△APB,
∴PB=MN
易得△APM、△ABN都是等边三角形,
∴PA=PM
∴PA+PB+PC=PM+MN+PC=CN,
∴BN=AB=6,∠BNA=60°,∠PAM=60°
∴∠CAN=∠CAB+∠BAN=60°+60°=120°,
∴∠CBN=90°
在Rt△ABC中,易得![]()
∴在Rt△BCN中, ![]()
“点睛”本题属于几何变换综合题,主要考查了旋转和平移的性质、全等三角形的判定和性质、矩形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造等边三角形和全等三角形,依据图形的性质进行计算求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=2,ab=1,则a2 + b2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为
 cm,双层部分的长度为
cm,双层部分的长度为 cm,经测量,得到如下数据:
cm,经测量,得到如下数据:(1)根据表中数据的规律,完成以下表格(填括号),并直接写出
 关于
关于 的函数解析式;
的函数解析式;单层部分的长度
 (cm)
(cm)…
4
6
8
10
…
150
双层部分的长度
 (cm)
(cm)…
73
72
71
( )
…
( )
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;

(3)设挎带的长度为
 cm,求
cm,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.正数、负数统称为有理数
B.小数-3.14不是分数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s.在跑步过程中,甲、乙两人的距离y(单位:m)与乙出发的时间t(单位:s)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
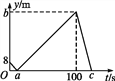
A. ①② B. ②③
C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知顶点为A(2,﹣1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,0);
(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求
 的大小;
的大小;(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形不是立体图形的是( )
A.球
B.圆柱
C.圆锥
D.圆
相关试题

