【题目】已知顶点为A(2,﹣1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,0);
(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求![]() 的大小;
的大小;
(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
参考答案:
【答案】(1)y=x2﹣4x+3 (2)![]() (3)点P(3+
(3)点P(3+![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x-2)2-1,将点C的坐标代入可求得a的值,从而可得到抛物线的解析式;
(2)先求得点B、C、D的坐标,由点A、B、D的坐标可得到∠BDO=∠ADO=45°,从而可证明△ABD为直角三角形,然后依据两点间的距离公式可求得AB和BD的长,最后依据余弦定理的定义求解即可;
(3)先证明△ADP∽△PDB,依据相似三角形的性质可得到DP2=BD×AD,从而可求得DP的长,故此可得到点P的坐标.
解:(1)∵顶点为A(2,﹣1)的抛物线经过点C(1,0),

∴可以假设抛物线的解析式为y=a(x﹣2)2﹣1,
把(1,0)代入可得a=1,
∴抛物线的解析式为y=x2﹣4x+3.
(2)令y=0,x2﹣4x+3=0,解得x=1或3,
∴C(1,0),D(3,0),令x=0,y=3,
∴B(0,3)∵OB=OD=3,∴∠BDO=45°,
∵A(2,﹣1),D(3,0),
∴∠ADO=45°,∴∠BDA=90°,∴![]() ·
·
(3)∵∠BDO=∠DPB+∠DBP=45°,∠APB=∠DPB+∠DPA=45°,∴∠DBP=∠APD,
∵∠PDB=∠ADP=135°,∴△PDB∽△ADP,∴PD2=BDAD=3![]() ×
×![]() =6,
=6,
∴PD=![]() ,∴OP=3+
,∴OP=3+![]() ,∴点P(3+
,∴点P(3+![]() ,0).
,0).
“点睛”本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义、学生三角形的性质和判断,证得△ABD为直角三角形是解答问题(2)的关键;证得△ADP∽△PDB是解答问题(3)的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.正数、负数统称为有理数
B.小数-3.14不是分数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、
A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,
AB=6时,根据此图求PA+PB+PC的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500 m,先到终点的人原地休息.已知甲先出发2 s.在跑步过程中,甲、乙两人的距离y(单位:m)与乙出发的时间t(单位:s)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
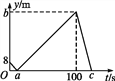
A. ①② B. ②③
C. ①③ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形不是立体图形的是( )
A.球
B.圆柱
C.圆锥
D.圆 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方形的长为2a+3b,宽为2b,则它的面积为_________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.16人
B.14人
C.4人
D.6人
相关试题

