【题目】某商场购进一种每件价格为6元的新商品,在商场试销发现:销售单价![]() (元/件)与每天销售量
(元/件)与每天销售量![]() (件)之间满足如图所示的关系:
(件)之间满足如图所示的关系:
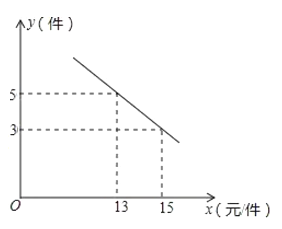
(1)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)若你是商场负责人,要使每天的利润达到35元,应将售价定为多少?
参考答案:
【答案】(1)y=-x+18;(2)售价定为13元/件或11元/件时,每天的利润能达到35元.
【解析】
(1)待定系数法求解可得;
(2)根据“每件利润×销售量=总利润”列出一元二次方程,解之可得.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),
由所给函数图象可得:![]() ,
,
解得:![]() ,
,
故y与x的函数关系式为y=-x+18;
(2)设每天的利润为W,由题意可得:
W=y(x-6)=(-x+18)(x-6)=-x2+24x-108=-(x-12)2+36,
令W=35,-(x-12)2+36=35,
解得:x=13或x=11,
故售价定为13元/件或11元/件时,每天的利润能达到35元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角,(本题中所有角都是指大于0°且小于180°的角)
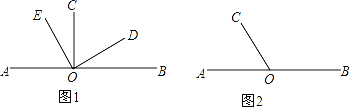
(1)如图1所示,O为直线AB上一点,OC⊥AB,OE⊥OD,图中哪些角互为垂角?(写出所有情况)
(2)如图2所示,O为直线AB上一点,∠AOC=60°,将∠AOC绕点O顺时针旋转n°(0°<n<120),OA旋转得到OA′,OC旋转得到OC′,当n为何值时,∠AOC′与∠BOA′互为垂角?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 内有一点
内有一点 满足
满足 ,
, .连接
.连接 、
、 .
.
(1)求证:
 ;
;(2)求
 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B、C、D、E、F六个球队进行单循环比赛(每两队之间赛一场,比赛结果必须分出胜负),每天同时在三个场地各进行一场比赛,前四天的积分表如下(E、F的积分被遮挡):
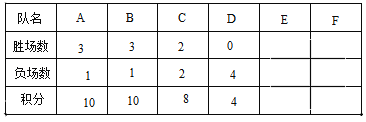
(1)根据积分榜,胜一场积几分,负一场积几分?
(2)若E队前四天积分比F队多4分,问E、F两队前四天的战绩分别是几胜几负?
(3)已知第一天B与D对阵,第二天C与E对阵,第三天D与F对阵,第四天B与C对阵,试分析第五天A和谁对阵比赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D
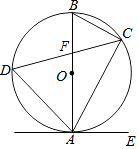
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ,CF=
,CF= 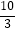 ,求BF的长.
,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+
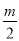 ﹣
﹣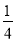 =0的两个实数根.
=0的两个实数根.(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 是
是 的中点,
的中点, 是
是 的中点,过点
的中点,过点 作
作 交
交 的延长线于点
的延长线于点 .
.
(1)求证:
 ;
;(2)求证:四边形
 是菱形;
是菱形;(3)若
 ,
, ,求菱形
,求菱形 的面积.
的面积.
相关试题

