【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
参考答案:
【答案】(1)见解析;(2)见解析(3)24
【解析】
(1)利用平行线的性质及中点的定义,可利用AAS证得结论;
(2)由(1)可得AF=BD,结合条件可求得AF=DC,则可证明四边形ADCF为平行四边形,再利用直角三角形的性质可证得AD=CD,可证得四边形ADCF为菱形;
(3)连接DF,可证得四边形ABDF为平行四边形,则可求得DF的长,利用菱形的面积公式可求得答案.
解:(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AFE和△DBE中,
 ,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵AD为BC边上的中线
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
(3)连接DF,
∵AF∥BD,AF=BD,![]() ,
,![]() ,
,
∴四边形ABDF是平行四边形,
∴DF=AB=8,
∵四边形ADCF是菱形,
∴S菱形ADCF=![]() AC×DF=
AC×DF=![]() ×6×8=24.
×6×8=24.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种每件价格为6元的新商品,在商场试销发现:销售单价
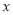 (元/件)与每天销售量
(元/件)与每天销售量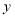 (件)之间满足如图所示的关系:
(件)之间满足如图所示的关系: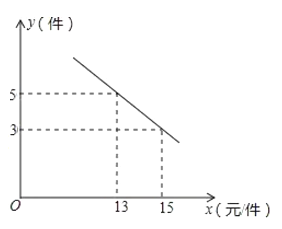
(1)求出
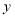 与
与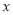 之间的函数关系式.
之间的函数关系式.(2)若你是商场负责人,要使每天的利润达到35元,应将售价定为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D
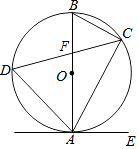
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD= ,CF=
,CF= 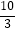 ,求BF的长.
,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+
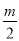 ﹣
﹣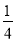 =0的两个实数根.
=0的两个实数根.(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么ABCD的周长是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )

A.BE=4
B.∠F=30°
C.AB∥DE
D.DF=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1 , △AB1C的面积为S2 , 则S1 , S2的大小关系为( )

A.S1>S2
B.S1=S2
C.S1<S2
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于
中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点.点A关于原点O的对称点A′,点B关于 轴的对称点为B′,点C关于
轴的对称点为B′,点C关于 轴的对称点为C′.
轴的对称点为C′.(1)A′的坐标为 ,B′的坐标为 ,C′的坐标为 .
(2)建立平面直角坐标系,描出以下三点A、B′、C′,并求△AB′C′的面积.
相关试题

