【题目】杭州某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下: 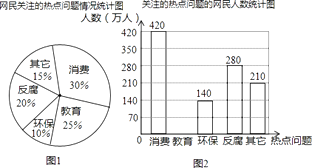
根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若杭州市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为
参考答案:
【答案】
(1)解:调查的总人数是:420÷30%=1400(人),
关注教育的人数是:1400×25%=350(人).
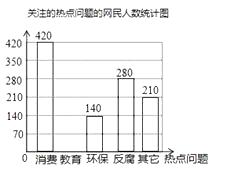
(2)解:900×10%=90万人
(3)![]()
【解析】解: (3)画树形图得: 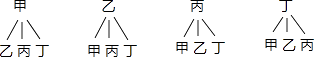
则P(抽取的两人恰好是甲和乙)= ![]() =
= ![]() .
.
故答案为: ![]() .
.
(1)根据关注消费的人数是420人,所占的比例式是30%,即可求得总人数,然后利用总人数乘以关注教育的比例求得关注教育的人数;(2)利用总人数乘以对应的百分比即可;(3)利用列举法即可求解即可.
-
科目: 来源: 题型:
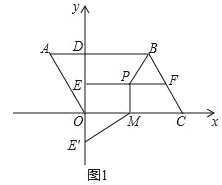
查看答案和解析>>【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
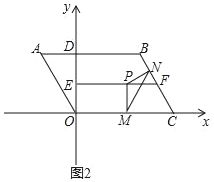
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳果品店在批发市场购买某种水果销售,第一次用1200元购进若干千克,并以每千克8元出售,很快售完.由于水果畅销,第二次购买时,每千克的进价比第一次提高了10%,用1452元所购买的数量比第一次多20千克,以每千克9元售出100千克后,因出现高温天气,水果不易保鲜,为减少损失,便降价50%售完剩余的水果.
(1)求第一次水果的进价是每千克多少元?
(2)该果品店在这两次销售中,总体上是盈利还是亏损?盈利或亏损了多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.

(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP= ,求NQ的长.
,求NQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图像与反比例函数y=
 的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D. 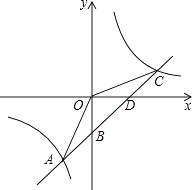
(1)求反比例函数y= 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.、 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣  x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C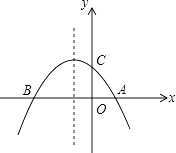
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
相关试题

