【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() 的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D. 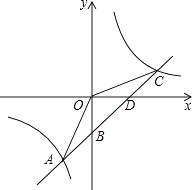
(1)求反比例函数y= ![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.、
参考答案:
【答案】
(1)解:把A(﹣2,﹣5)代入y= ![]() 得:﹣5=
得:﹣5= ![]() ,
,
解得:m=10,
则反比例函数的解析式是:y= ![]() ,
,
把x=5代入,得:y= ![]() =2,
=2,
则C的坐标是(5,2).
根据题意得: ![]() ,
,
解得: ![]() ,
,
则一次函数的解析式是:y=x﹣3
(2)解:在y=x﹣3中,令x=0,解得:y=﹣3.
则B的坐标是(0,﹣3).
∴OB=3,
∵点A的横坐标是﹣2,C的横坐标是5.
∴S△AOC=S△AOB+S△BOC= ![]() OB×2×5+
OB×2×5+ ![]() ×OB×5=
×OB×5= ![]() ×3×7=
×3×7= ![]()
【解析】(1)把A(﹣2,﹣5)代入y= ![]() 求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式;(2)首先求得C的坐标,根据S△AOC=S△AOB+S△BOC即可求解.
求得m的值,然后求得C的坐标,利用待定系数法求得直线的解析式;(2)首先求得C的坐标,根据S△AOC=S△AOB+S△BOC即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MN是⊙O的直径,直线PQ与⊙O相切于P点,NP平分∠MNQ.

(1)求证:NQ⊥PQ;
(2)若⊙O的半径R=2,NP= ,求NQ的长.
,求NQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】杭州某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:
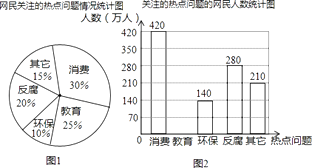
根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若杭州市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( ).

A. OA=OC,OB=OD B. ∠BAD=∠BCD,AB∥CD
C. AD∥BC,AD=BC D. AB=CD,AO=CO
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣  x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C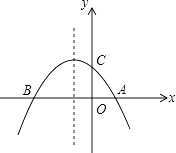
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l和双曲线
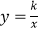 (k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( )
(k>0)交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别是C,D,E,连接OA,OB,OP,设△AOC面积是S1 , △BOD面积是S2 , △POE面积是S3 , 则( ) 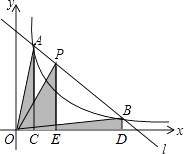
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
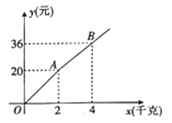
A. 4 B. 5 C. 6 D. 7
相关试题

