【题目】如图,![]() .
.

(1)如图①,在平面直角坐标系中,以![]() 为顶点,
为顶点,![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)如图②,![]() 为
为![]() 轴负半轴上一个动点,以
轴负半轴上一个动点,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,当
点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问![]() 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;
(3)如图③,已知点![]() 坐标为
坐标为![]() ,
,![]() 是
是![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 为直角边作等腰
为直角边作等腰![]() ,
,![]() 点在
点在![]() 轴上,
轴上,![]() ,设
,设![]() 、
、![]() ,当
,当![]() 点在
点在![]() 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,![]() 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由.
参考答案:
【答案】(1)C点的坐标为(-6,-2);(2)OP-DE的值不变,值为2;(3)m+n的和不变,值为-8.
【解析】
(1)作CD⊥x轴于D,证明△ACD≌△BAO,根据全等三角形的性质得到DC=OA=2,AD=OB=4,计算即可;
(2)作DF⊥y轴于F,证明△APO≌△DPF,得到PF=OA=2,DF=OP,结合图形计算;
(3)作PM⊥x轴于M,PN⊥y轴于N,仿照(2)的证明过程解答.
解:(1)作CD⊥x轴于D,

∴∠ACD+∠CAD=90°,
∵∠CAB=90°,
∴∠BAO+∠CAD=90°,
∴∠BAO=∠ACD,
在△ACD和△BAO中,
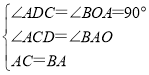 ,
,
∴△ACD≌△BAO,
∴DC=OA=2,AD=OB=4,
∴OD=6,
∴C点的坐标为(-6,-2);
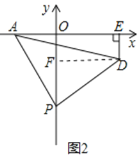
(2)OP-DE的值不变,值为2,
理由如下:作DF⊥y轴于F,
∴∠PDF+∠DPF=90°,
∵∠APD=90°,
∴∠APO+∠DPF=90°,
∴∠APO=∠PDF,
在△APO和△DPF中,
 ,
,
∴△APO≌△DPF,
∴PF=OA=2,DF=OP,
∴OP-DE=OP-OF=PF=2;
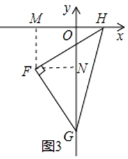
(3)m+n的和不变,值为-8,
理由如下:作PM⊥x轴于M,PN⊥y轴于N,
由(2)可知,△HNF≌△GNF,
∴GN=MH,FN=FM=OM=4,
m+n=-(OG-OH)=-(GN+ON-MH+OM)=-(ON+OM)=-8.
故答案为:(1)C点的坐标为(-6,-2);(2)OP-DE的值不变,值为2;(3)m+n的和不变,值为-8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为
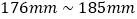 的产品为合格),随机各抽取了20个样品进行检测,过程如下:
的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:
 ):
):甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:

分析数据:
车间
平均数
众数
中位数
方差
甲车间
180
185
180
43.1
乙车间
180
180
180
22.6
应用数据:
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
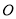 为坐标原点,
为坐标原点,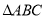 的顶点
的顶点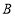 、
、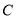 的坐标分别为
的坐标分别为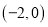 、
、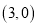 ,顶点
,顶点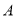 在
在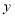 轴的正半轴上,
轴的正半轴上,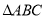 的高
的高 交线段
交线段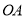 于点
于点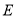 ,且
,且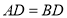 .
.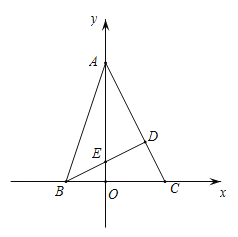
(1)求线段
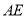 的长;
的长;(2)动点
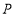 从点
从点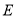 出发沿线段
出发沿线段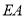 以每秒
以每秒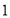 个单位长度的速度向终点
个单位长度的速度向终点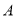 运动,动点
运动,动点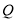 从点
从点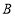 出发沿射线
出发沿射线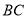 以每秒
以每秒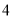 个单位长度的速度运动,
个单位长度的速度运动,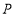 、
、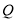 两点同时出发,且点
两点同时出发,且点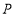 到达
到达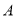 点处时
点处时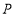 、
、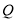 两点同时停止运动,设点
两点同时停止运动,设点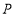 的运动时间为
的运动时间为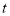 秒,
秒,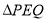 的面积为
的面积为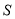 ,请用含
,请用含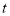 的式子表示
的式子表示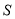 ,直接写出相应的
,直接写出相应的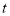 的取值范围;
的取值范围;(3)在(2)的条件下,点
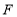 是直线
是直线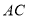 上的一点且
上的一点且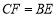 ,是否存在
,是否存在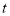 值,使以点
值,使以点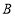 、
、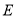 、
、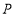 为顶点的三角形与以点
为顶点的三角形与以点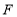 、
、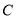 、
、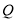 为顶点的三角形全等?若存在,请求出符合条件的
为顶点的三角形全等?若存在,请求出符合条件的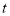 值,若不存在,请说明理由.
值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,滑动调节式遮阳伞的立柱
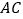 垂直于地面
垂直于地面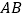 ,
,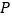 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为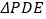 ,
,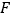 为
为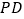 中点,
中点,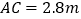 ,
,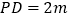 ,
,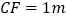 ,
,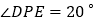 .当点
.当点 位于初始位置
位于初始位置 时,点
时,点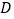 与
与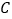 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与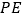 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.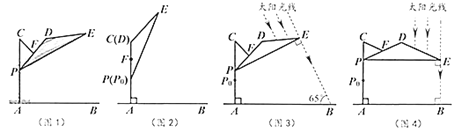
(1)上午10:00时,太阳光线与地面的夹角为
 (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点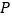 需从
需从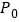 上调多少距离?(结果精确到
上调多少距离?(结果精确到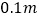 )
)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点
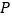 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到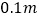 )
)(参考数据:
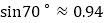 ,
,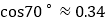 ,
,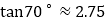 ,
,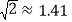 ,
,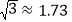 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
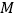 为二次函数
为二次函数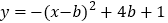 图象的顶点,直线
图象的顶点,直线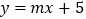 分别交
分别交 轴正半轴,
轴正半轴,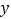 轴于点
轴于点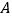 ,
,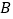 .
.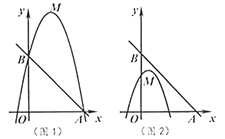
(1)判断顶点
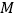 是否在直线
是否在直线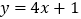 上,并说明理由.
上,并说明理由.(2)如图1,若二次函数图象也经过点
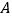 ,
,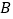 ,且
,且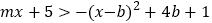 ,根据图象,写出
,根据图象,写出 的取值范围.
的取值范围.(3)如图2,点
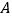 坐标为
坐标为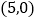 ,点
,点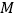 在
在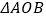 内,若点
内,若点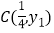 ,
,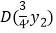 都在二次函数图象上,试比较
都在二次函数图象上,试比较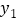 与
与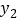 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
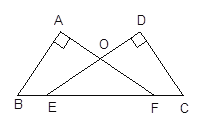
求证:(1)Rt△ABF≌Rt△DCE;(2)OE=OF .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
相关试题

