【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
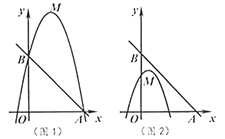
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
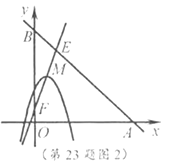
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
参考答案:
【答案】(1)点![]() 在直线
在直线![]() 上,理由见解析;(2)
上,理由见解析;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .(3)①当
.(3)①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() .
.
【解析】(1)写出点![]() 的坐标,代入直线
的坐标,代入直线![]() 进行判断即可.
进行判断即可.
(2)直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,求出点
,求出点![]() 坐标,把
坐标,把![]() 在抛物线上,代入求得
在抛物线上,代入求得![]() ,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出
,求出二次函数表达式,进而求得点A的坐标,数形结合即可求出![]() 时,
时,![]() 的取值范围.
的取值范围.
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,而直线
,而直线![]() 表达式为
表达式为![]() ,联立方程组
,联立方程组![]() ,得
,得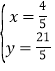 .点
.点![]() ,
,![]() .分三种情况进行讨论.
.分三种情况进行讨论.
【解答】
(1)∵点![]() 坐标是
坐标是![]() ,
,
∴把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
(2)如图1,∵直线![]() 与
与![]() 轴交于点为
轴交于点为![]() ,∴点
,∴点![]() 坐标为
坐标为![]() .
.
又∵![]() 在抛物线上,
在抛物线上,
∴![]() ,解得
,解得![]() ,
,
∴二次函数的表达式为![]() ,
,
∴当![]() 时,得
时,得![]() ,
,![]() ,∴
,∴![]() .
.
观察图象可得,当![]() 时,
时,
![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
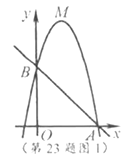
(3)如图2,∵直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
而直线![]() 表达式为
表达式为![]() ,
,
解方程组![]() ,得
,得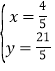 .∴点
.∴点![]() ,
,![]() .
.
∵点![]() 在
在![]() 内,
内,
∴![]() .
.
当点![]() ,
,![]() 关于抛物线对称轴(直线
关于抛物线对称轴(直线![]() )对称时,
)对称时,
![]() ,∴
,∴![]() .
.
且二次函数图象的开口向下,顶点![]() 在直线
在直线![]() 上,
上,
综上:①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
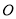 为坐标原点,
为坐标原点,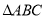 的顶点
的顶点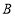 、
、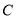 的坐标分别为
的坐标分别为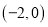 、
、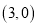 ,顶点
,顶点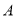 在
在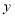 轴的正半轴上,
轴的正半轴上,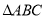 的高
的高 交线段
交线段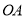 于点
于点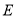 ,且
,且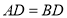 .
.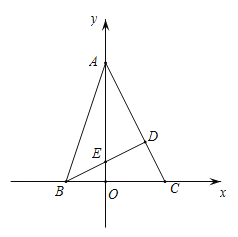
(1)求线段
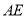 的长;
的长;(2)动点
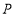 从点
从点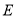 出发沿线段
出发沿线段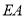 以每秒
以每秒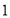 个单位长度的速度向终点
个单位长度的速度向终点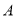 运动,动点
运动,动点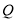 从点
从点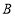 出发沿射线
出发沿射线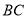 以每秒
以每秒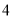 个单位长度的速度运动,
个单位长度的速度运动,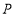 、
、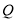 两点同时出发,且点
两点同时出发,且点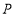 到达
到达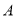 点处时
点处时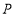 、
、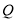 两点同时停止运动,设点
两点同时停止运动,设点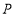 的运动时间为
的运动时间为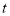 秒,
秒,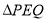 的面积为
的面积为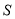 ,请用含
,请用含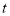 的式子表示
的式子表示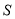 ,直接写出相应的
,直接写出相应的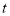 的取值范围;
的取值范围;(3)在(2)的条件下,点
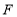 是直线
是直线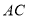 上的一点且
上的一点且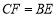 ,是否存在
,是否存在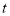 值,使以点
值,使以点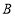 、
、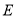 、
、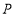 为顶点的三角形与以点
为顶点的三角形与以点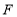 、
、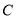 、
、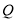 为顶点的三角形全等?若存在,请求出符合条件的
为顶点的三角形全等?若存在,请求出符合条件的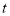 值,若不存在,请说明理由.
值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,滑动调节式遮阳伞的立柱
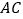 垂直于地面
垂直于地面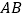 ,
,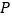 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为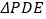 ,
,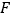 为
为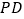 中点,
中点,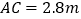 ,
,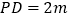 ,
,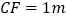 ,
,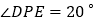 .当点
.当点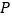 位于初始位置
位于初始位置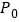 时,点
时,点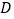 与
与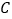 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与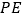 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.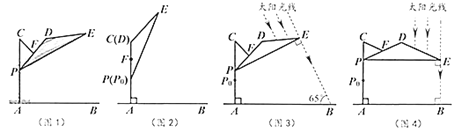
(1)上午10:00时,太阳光线与地面的夹角为
 (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点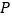 需从
需从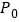 上调多少距离?(结果精确到
上调多少距离?(结果精确到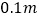 )
)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点
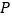 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到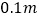 )
)(参考数据:
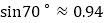 ,
,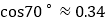 ,
,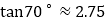 ,
,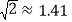 ,
,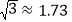 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
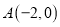 .
.
(1)如图①,在平面直角坐标系中,以
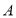 为顶点,
为顶点,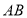 为腰在第三象限作等腰
为腰在第三象限作等腰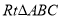 ,若
,若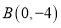 ,求
,求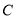 点的坐标;
点的坐标;(2)如图②,
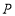 为
为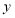 轴负半轴上一个动点,以
轴负半轴上一个动点,以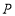 为顶点,
为顶点,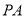 为腰作等腰
为腰作等腰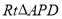 ,过
,过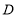 作
作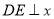 轴于
轴于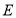 点,当
点,当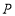 点沿
点沿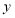 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问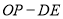 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;(3)如图③,已知点
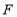 坐标为
坐标为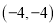 ,
,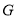 是
是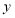 轴负半轴上一点,以
轴负半轴上一点,以 为直角边作等腰
为直角边作等腰 ,
,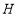 点在
点在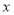 轴上,
轴上,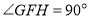 ,设
,设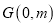 、
、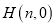 ,当
,当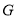 点在
点在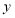 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,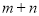 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
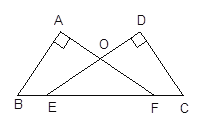
求证:(1)Rt△ABF≌Rt△DCE;(2)OE=OF .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第①小题的计算方法,再计算第②小题.
①–5
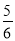 +(–9
+(–9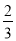 )+17
)+17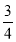 +(–3
+(–3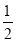 )
)解:原式=[(–5)+(–
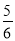 )]+[(–9)+(–
)]+[(–9)+(–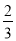 )]+(17+
)]+(17+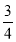 )+[(–3+(–
)+[(–3+(–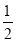 )]
)]=[(–5)+(–9)+(–3)+17]+[(–
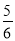 )+(–
)+(–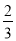 )+(–
)+(–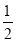 )+
)+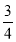 ]
]=0+(–1
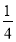 )
)=–1
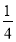 .
.上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000
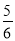 )+(﹣1999
)+(﹣1999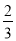 )+4000
)+4000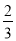 +(﹣1
+(﹣1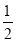 )
)
相关试题

