【题目】已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF与AC交于点N.
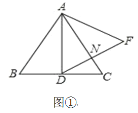
(1)如图①,当AD⊥BC时,请说明DF⊥AC的理由;
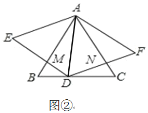
(2)如图②,当点D在BC上移动时,以AD为边再向左作等边△ADE,DE与AB交于点M,试问线段AM和AN有什么数量关系?请说明你的理由;
(3)在(2)的基础上,若等边△ABC的边长为2,直接写出DM+DN的最小值.
参考答案:
【答案】(1)详见解析;(2)AM=AN,理由详见解析;(3)![]()
【解析】
(1)根据等腰三角形三线合一的性质可得∠CAD=30°,再求出∠FAN=30°,然后根据等腰三角形三线合一的性质证明;
(2)根据等边三角形的每一个角都是60°可得∠ADE=∠ADF,等边三角形的三条边都相等可得AD=AF,再求出∠DAM=∠FAN,然后利用“角边角”证明△ADM和△AFN全等,根据全等三角形对应边相等即可得到AM=AN;
(3)根据垂线段最短可得DM⊥AB、DN⊥AC时,DM、DN最短,再利用△ABC的面积求出此时DM+DN等于等边△ABC的高,然后求解即可.
(1)证明:∵△ABC是等边三角形,AD⊥BC,
∴∠CAD=![]() ×60°=30°,
×60°=30°,
又∵△ADF是等边三角形,
∴∠DAF=60°,
∴∠DAN=∠FAN=30°,
∴AN⊥DF,
即DF⊥AC;
(2)AM=AN,理由如下:
∵△ADE,△ADF是等边三角形,
∴∠ADE=∠F=60°,AD=AF,
∵∠DAM+∠CAD=60°,
∠FAN+∠CAD=60°,
∴∠DAM=∠FAN,
在△ADM和△AFN中,
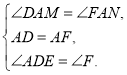
∴△ADM≌△AFN(ASA),
∴AM=AN;
(3)根据垂线段最短,DM⊥AB,DN⊥AC时,DM,DN最短,设等边△ABC的高线为h,
则![]() ,
,
![]() ,
,
∴S△ABC=![]() ACh=
ACh=![]() AC(DM+DN),
AC(DM+DN),
∴DM+DN=h,
∵等边△ABC的边长为2,
![]() .
.
∴DM+DN的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块土地,如图所示,已知AB=8,
 ,BC=6,CD=24,AD=26,求这块土地的面积.
,BC=6,CD=24,AD=26,求这块土地的面积.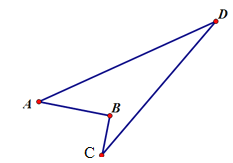
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.

(1)若某月用水量为18立方米,则应交水费多少元?
(2)当用水18立方米以上时,每立方米应交水费多少元?
(3)若小敏家某月交水费81元,则这个月用水量为多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
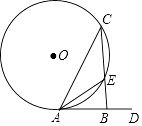
查看答案和解析>>【题目】如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=
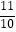 ,则tan∠BAD= .
,则tan∠BAD= . 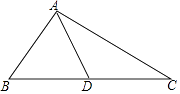
相关试题

