【题目】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF
⑴求证:四边形ABCD是平行四边形.
⑵若∠BAE=∠BDC,AE=3,BD=9,AB=4,求四边形ABCD的周长.

参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由垂直得到∠EAD=∠FCB=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形的判定判断即可;
(2)由平行四边形ABCD的性质可得:AB//CD,从而得到∠ABE=∠BDC,又由∠BAE=∠BDC可得:∠ABE=∠BAE,从而得出BE=AE=3,DE=BD-BE=6,在Rt△AED中,根据勾股定理求得AD的长度,再求其周长即可.
(1)∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
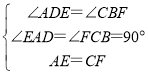 ,
,
∴Rt△AED≌Rt△CFB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB//CD,
∴∠ABE=∠BDC,
又∵∠BAE=∠BDC,
∴∠ABE=∠BAE,
∴BE=AE=3,
∴DE=BD-BE=6,
在Rt△AED中,AD=![]() ,
,
∴四边形ABCD的周长为2(![]() +4)=
+4)=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填在相应的横线上
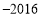 ,
, ,
, ,
, ,
,  ,
, ,
,  ,
,  ,π
,π 负有理数:________________________________
分数: ____________________________________
整数: ____________________________________
非负数: ___________________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线MN//PQ,直线AC交MN、PQ于点A、C,所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.试猜想AC与BD的关系,并说明理由.
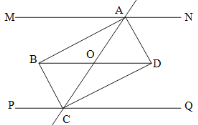
-
科目: 来源: 题型:
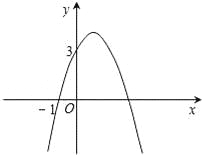
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有三点A、B、C,请根据图回答下列问题:

(1)若将点B向左平移3个单位后,则A、B、C这三个点所表示的数谁最小?是多少?
(2)若将点A向右平移4个单位后,则A、B、C这三个点所表示的数谁最大?最大的数比最小的数大多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
相关试题

