【题目】关于x的方程x2﹣(2m﹣1)x+m2﹣1=0的两实数根为x1 , x2 , 且x12+x22=3,则m= .
参考答案:
【答案】0
【解析】解:∵方程x2﹣(2m﹣1)x+m2﹣1=0的两实数根为x1 , x2 , ∴x1+x2=2m﹣1,x1x2=m2﹣1,
∵x12+x22=(x1+x2)2﹣2x1x2=(2m﹣1)2﹣2(m2﹣1)=3,
解得:m1=0,m2=2,
∵方程有两实数根,
∴△=(2m﹣1)2﹣4(m2﹣1)≥0,
即m≤ ![]()
∴m2=2(不合题意,舍去),
∴m=0;
所以答案是:0.
【考点精析】掌握求根公式和根与系数的关系是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).
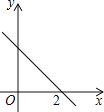
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B均在函数y=
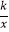 (k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( )
(k>0,x>0)的图象上,⊙A与x轴相切,⊙B与y轴相切.若点B的坐标为(1,6),⊙A的半径是⊙B的半径的2倍,则点A的坐标为( ) 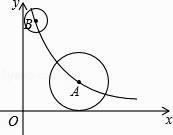
A.(2,2)
B.(2,3)
C.(3,2)
D.(4, )
) -
科目: 来源: 题型:
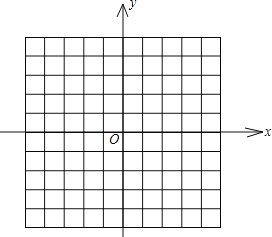
查看答案和解析>>【题目】在如图的坐标系中,画出函数y=2与y=2x+6的图象,并结合图象求:
(1)方程2x+6=0的解;
(2)不等式2x+6>2的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)20170﹣|﹣sin45°|cos45°+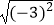 ﹣(﹣
﹣(﹣  )﹣1
)﹣1
(2) .
.
相关试题

