【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
参考答案:
【答案】(1)图形见解析(2)![]()
【解析】
试题分析:(1)根据题意按要求逐步画图即可;
(2)连接AA’,然后根据旋转的性质和勾股定理可求解.
试题解析:(1)按要求画图,如图所示.
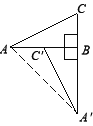
(2)连接A A′.
∵在Rt△ABC中,∠ABC=90°,BC=1,AC=![]() ,
,
∴由勾股定理得AB=2.
∵以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,
∴A′B=AB=2.
∵在Rt△ABA′中,∠ABA′=90°,A′B=AB=2,
∴由勾股定理得AA′=![]()
∴点A和点A′之间的距离是![]()
-
科目: 来源: 题型:
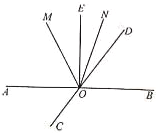
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
(1)若∠MOE=27°,求∠AOC的度数;
(2)当∠BOD=x°(0<x<90)时,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
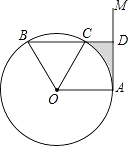
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积(结果保留π和根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个大圆盘中,镶嵌着四个大小一样的小圆盘,已知大小圆盘的半径都是整数,阴影部分的面积为5πcm2 , 请你求出大小两个圆盘的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=_______,△APE的面积等于8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=4.8cm,点C是线段AB的中点,点D是线段CB的中点,点E在线段AB上,且CE=
 AC,画图并计算DE的长.
AC,画图并计算DE的长.
相关试题

