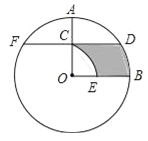
【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
参考答案:
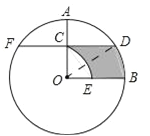
【答案】(1)2;(2)![]() .
.
【解析】
试题分析:(1)首先证明OA⊥DF,由OD=2CO推出∠CDO=30°,设OC=x,则OD=2x,利用勾股定理即可解决问题;
(2)根据S圆=S△CDO+S扇形OBD﹣S扇形OCE计算即可.
试题解析:解;(1)连接OD,∵OA⊥OB,∴∠AOB=90°,∵CD∥OB,∴∠OCD=90°,在RT△OCD中,∵C是AO中点,CD=![]() ,∴OD=2CO,设OC=x,∴
,∴OD=2CO,设OC=x,∴![]() ,∴x=1,∴OD=2,∴⊙O的半径为2;
,∴x=1,∴OD=2,∴⊙O的半径为2;
(2)∵sin∠CDO=![]() =
=![]() ,∴∠CDO=30°,∵FD∥OB,∴∠DOB=∠ODC=30°,∴S圆=S△CDO+S扇形OBD﹣S扇形OCE
,∴∠CDO=30°,∵FD∥OB,∴∠DOB=∠ODC=30°,∴S圆=S△CDO+S扇形OBD﹣S扇形OCE
=![]() =
=![]() .
.
-
科目: 来源: 题型:
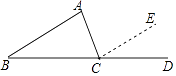
查看答案和解析>>【题目】如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合
B.特殊到一般
C.一般到特殊
D.转化 -
科目: 来源: 题型:
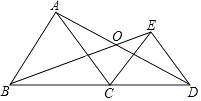
查看答案和解析>>【题目】如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是( )
A.对角线互相垂直的四边形是菱形
B.中心对称图形都是轴对称图形
C.三角形的一个外角大于它的内角
D.数据2,3,1,2的方差是0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=(x﹣1)2﹣2
D.y=(x+1)2﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=
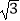 ,则BC= .
,则BC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b是方程x2﹣2x﹣3=0的两个实数根,则a2+b2=________.
相关试题

