【题目】如图,△ABC与△ECD都是等边三角形,AB≠EC,下列结论中:①BE=AD;②∠BOD=120°;③OA=OD.正确的序号是 . 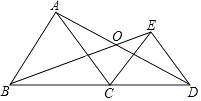
参考答案:
【答案】①②
【解析】解:∵△ABC和△ECD都是等边三角形, ∴BC=AC,CE=CD,∠BCA=∠ECD=∠BAC=60°,
∴∠BCA+∠ACE=∠ECD+∠ACE,
∵∠BCE=∠ACD,
在△BCE和△ACD中,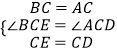 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,故①正确.
∵∠AOB=∠EBC+∠ADC,
∴∠AOB=∠EBC+∠BEC=∠DCE=60°.
∵∠AOB+∠BOD=180°,
∴∠BOD=120°,故②正确,
不能证明OA=OD,③错误,
故选:①②.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
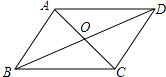
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AD∥BC,AD=BC
D.∠BAD=∠BCD,AB∥CD -
科目: 来源: 题型:
查看答案和解析>>【题目】据中国电子商务研究中心监测数据显示,2015年第一季度中国轻纺城市场群的商品成交额达27 800 000 000元,将27 800 000 000用科学记数法表示为( )
A.2.78×1010
B.2.78×1011
C.27.8×1010
D.0.278×1011 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
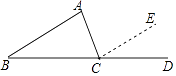
A.数形结合
B.特殊到一般
C.一般到特殊
D.转化 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是( )
A.对角线互相垂直的四边形是菱形
B.中心对称图形都是轴对称图形
C.三角形的一个外角大于它的内角
D.数据2,3,1,2的方差是0.5
-
科目: 来源: 题型:
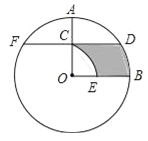
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
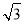 ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作 ,交OB于E点.
,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=(x﹣1)2﹣2
D.y=(x+1)2﹣2
相关试题

