【题目】化简:cos21°+cos22°+cos23°+…+cos289°.
参考答案:
【答案】解:cos21°+cos22°+cos23°+…+cos289°
=cos21°+cos289°+…+cos244°+cos246°+cos245°
=(cos21°+cos289°)+…+(cos244°+cos246°)+( ![]() )2
)2
= ![]() +
+ ![]()
=44 ![]()
【解析】根据锐角三角函数关系式:互为余角的两个角的余弦平方和等于1.
还要注意cos45°= ![]() .
.
【考点精析】本题主要考查了互余两角的三角函数关系的相关知识点,需要掌握互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,击打台球时小球反弹前后的运动路线遵循对称原理,即小球反弹前后的运动路线与台球案边缘的夹角相等(α=β),在一次击打台球时,把位于点P处的小球沿所示方向击出,小球经过5次反弹后正好回到点P,若台球案的边AD的长度为4,则小球从P点被击出到回到点P,运动的总路程为( )

A.16
B.16
C.20
D.20
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
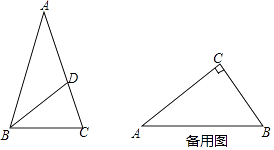
(1)等边三角形“內似线”的条数为;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,
 = 。
= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述
①单项式-
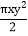 的系数是-
的系数是- ,次数是3次;
,次数是3次;②用一个平面去截一个圆锥,截面的形状可能是一个三角形;
③在数轴上,点A、B分别表示有理数a、b,若a>b,则A到原点的距离比B到原点的距离大;
④从八边形的一个顶点出发,最多可以画五条对角线;
⑤六棱柱有八个面,18条棱.
其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
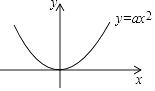
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO. -
科目: 来源: 题型:
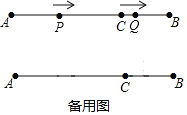
查看答案和解析>>【题目】如图,AB=12cm,点C在线段AB上,AC=3BC,动点P从点A出发,以4cm/s的速度向右运动,到达点B之后立即返回,以4cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动,到达点B之后立即返回,以1cm/s的速度向左运动.设它们同时出发,运动时间为t秒,当第二次重合时,P、Q两点停止运动.
(1)AC=______cm,BC=______cm;
(2)当t=______秒时,点P与点Q第一次重合;当t=______秒时,点P与点Q第二次重合;
(3)当t为何值时,AP=PQ?
相关试题

