【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a﹣3b|+(a+b﹣4)2=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,![]() = 。
= 。

参考答案:
【答案】(1)a=3,b=1;
(2)当t=10秒或85秒时,两灯的光束互相平行;
(3)∠BAC:∠BCD=3:2
【解析】分析:
(1)根据|a-3b|+![]() =0,可得a-3b=0,且a+b-4=0,进而得出a、b的值;
=0,可得a-3b=0,且a+b-4=0,进而得出a、b的值;
(2)设A灯转动x秒,两灯的光束互相平行,分两种情况进行讨论:①在灯A射线转到AN之前,②在灯A射线转到AN之后,分别求得t的值即可;
(3)设灯A射线转动时间为t秒,根据∠BAC=45°-(180°-3t)=3t-135°,∠BCD=90°-∠BCA=90°-(180°-2t)=2t-90°,可得∠BAC与∠BCD的数量关系.
本题解析:(1)∵a、b满足|a﹣3b|+(a+b﹣4)2=0,
∴a﹣3b=0,且a+b﹣4=0,
∴a=3,b=1;
(2)设A灯转动x秒,两灯的光束互相平行,
①在灯A射线转到AN之前,
3t=(20+t)×1 解得t=10;
②在灯A射线转到AN之后,
3t﹣3×60+(20+t)×1=180, 解得t=85
综上所述,当t=10秒或85秒时,两灯的光束互相平行;
(3)(3)设灯A射线转动时间为t秒,
∵∠CAN=![]() 3t,
3t,
∴∠BAC=![]() (
(![]() 3t)=3t
3t)=3t![]() ,
,
又∵PQ∥MN,
∴∠BCA=∠CBD+∠CAN=t+![]() 3t=
3t=![]() 2t,
2t,
而∠ACD=![]() ,
,
∴∠BCD=![]() ∠BCA=
∠BCA=![]() (
(![]() 2t)=2t
2t)=2t![]() ,
,
∴![]() ,
,
-
科目: 来源: 题型:
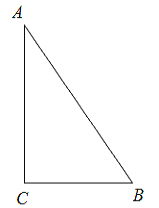
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)问t满足什么条件时,△BCP为直角三角形;
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】沿着一条公路栽树,第一棵栽在路的始端,以后每隔50米栽一棵,要求路的末端栽一棵,这样,缺少21棵树;如果每隔55米栽一棵,要求在路的末端栽一棵,这样,只缺少一棵树.求树的棵数和这条公路的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空:
(1)乘积是1的两个数互为______;
(2)有理数的除法法则,除以一个数等于乘以这个数的______;
(3)两数相除,同号得______,异号得______,并把绝对值______,0除以任何一个不等于0的数都得______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-a-b)(a-b)等于_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  ,点
,点 在线段
在线段 上运动(D不与B、C重合),连接AD,作
上运动(D不与B、C重合),连接AD,作 ,
,  交线段
交线段 于
于 .
.(1)当
 时,
时,  ____________°, ∠DEC ____________°;点D从B向C运动时,
____________°, ∠DEC ____________°;点D从B向C运动时,  逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);(2)当
 等于多少时,
等于多少时,  ≌
≌ ,请说明理由;
,请说明理由; (3)在点D的运动过程中,
 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出 的度数.若不可以,请说明理由。
的度数.若不可以,请说明理由。
相关试题

