【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.

(1)求证:△ABC∽△CBD;
(2)如果AC=4,BC=3,求BD的长.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)根据相似三角形的判定,由已知可证∠A=∠DCB,又因为∠ACB=∠BDC=90°,即证△ABC∽△CBD,
(2)根据勾股定理得到AB=5,根据三角形的面积公式得到CD=![]() ,然后根据勾股定理即可得到结论.
,然后根据勾股定理即可得到结论.
(1)证明:∵CD⊥AB,
∴∠BDC=90°.
∴∠A+∠ACD=90°.
∵∠ACB=90°,
∴∠DCB+∠ACD=90°.
∴∠A=∠DCB.
又∵∠ACB=∠BDC=90°,
∴△ABC∽△CBD;
(2)解:∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∴CD=![]() ,
,
∵CD⊥AB,
∴BD=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣2时,代数式x+1的值是( )
A.﹣1 B.﹣3 C.1 D.3
-
科目: 来源: 题型:
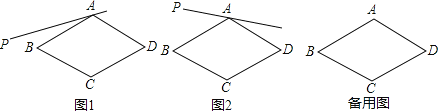
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
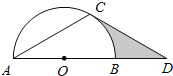
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x的值:
(1)(2x-1)2= 25 (2)3(x-4)3= -375
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将三角形各点的横坐标都加上4,纵坐标保持不变,所得图形与原图形相比( )
A. 向右平移了4个单位 B. 向左平移了4个单位
C. 向上平移了4个单位 D. 向下平移了4个单位
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2﹣2x+3化为y=(x﹣h)2+k的形式,结果为( )
A.y=(x+1)2+4 B.y=(x﹣1)2+4
C.y=(x+1)2+2 D.y=(x﹣1)2+2
相关试题

