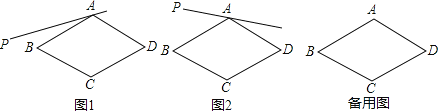
【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系.
参考答案:
【答案】(1)见解析;(2)∠ABF=∠ADF.见解析;(3)DF=ED﹣BF.见解析;(4)BF=DE+DF.
【解析】
试题分析:(1)根据题目要求补全图形即可;
(2)连接AE.由轴对称图形的性质可知EA=AB,∠ABF=∠AEF,由菱形的定义可知AB=AD,从而得到AE=AD,由等腰三角形的性质可知∠AEF=∠ADF,于是得到∠ABF=∠ADF;
(3)由轴对称图形的性质可知EF=BF,然后由DF=ED﹣EF,可知DF=ED﹣BF;
(4)由轴对称图形的性质可知EF=BF,然后由EF=ED+DF,可知BF=DE+DF.
解:(1)如图1所示:
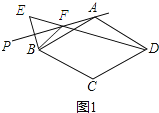
(2)∠ABF=∠ADF.
理由:如图2所示:连接AE.
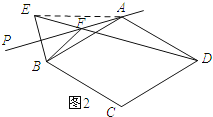
∵点B与点E关于直线PA对称,
∴EA=AB,∠ABF=∠AEF.
∵四边形ABCD为菱形,
∴AB=AD.
∴AE=AD.
∴∠AEF=∠ADF.
∴∠ABF=∠ADF.
(3)DF=ED﹣BF.
理由:如图3所示:
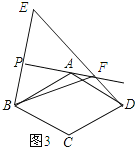
∵点B与点E关于PA对称,
∴EF=BF.
又∵DF=ED﹣EF,
∴DF=ED﹣BF.
(4)BF=DE+DF.
理由:如图4所示:
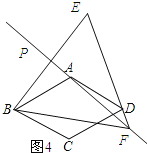
∵点B与点E关于PA对称,
∴EF=BF.
又∵EF=ED+DF,
∴BF=DE+DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列表述,能确定位置的是( )
A. 某电影院2排 B. 南京市大桥南路
C. 北偏东30° D. 东经118°,北纬40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】为保证中小学生每天锻炼一小时,涟水县某中学开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计图(1)和图(2).
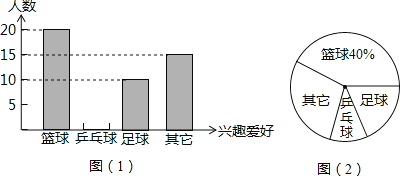
(1)某班同学的总人数为 人;
(2)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(3)扇形统计图(2)中表示”篮球”项目扇形的圆心角度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣2时,代数式x+1的值是( )
A.﹣1 B.﹣3 C.1 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
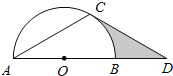
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.

(1)求证:△ABC∽△CBD;
(2)如果AC=4,BC=3,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x的值:
(1)(2x-1)2= 25 (2)3(x-4)3= -375
相关试题

