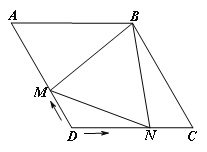
【题目】如图,菱形ABCD,∠A=60°,AB=6,点M从点D向点A以1个单位∕秒的速度运动,同时点N从点D向点C以2个单位∕秒的速度运动,连结BM、BN,当△BMN为等边三角形时,![]() =_____.
=_____.
参考答案:
【答案】![]()
【解析】
连接BD,证明△ABM≌△DBN,由此得到AM=DN,据此可求出运动时间为2秒,从而得到MD=2,DN=4.在△MDN中求出MN值,根据等边△面积公式即可求解.
解:连接BD,如图1所示:
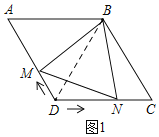
若△BMN是等边三角形,则BM=BN,∠MBN=60°.
∴∠DBN+∠MBD=60°.
∵四边形ABCD是菱形,∠A=60°,
∴AB=BD,∠ABD=60°.
∴∠ABM+∠MBD=60°,
∴∠ABM=∠DBN.
∴△ABM≌△DBN(SAS).
∴AM=DN.
设运动时间为t,则6-t=2t,解得t=2.
所以DM=2,DN=4.
如图2,过M点作MH⊥DN,交ND延长线于H点,
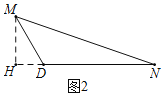
∵∠MDN=120°,
∴∠MDH=60°,
∴在Rt△MDH中,HD=![]() MD=1,MH=
MD=1,MH=![]() .
.
在Rt△MHN中,利用勾股定理可得MN=![]() .
.
∴等边三角形的边长为![]() .
.
∴等边三角形BMN的面积=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.
 C.2或
C.2或 D.2或
D.2或
-
科目: 来源: 题型:
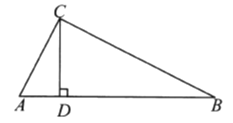
查看答案和解析>>【题目】如图,在
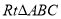 中,
中, 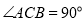 ,CD是斜边AB上的高.
,CD是斜边AB上的高.(1)证明:
 ∽
∽
(2)写出除(1)外的另两对相似三角形.
(3)AC是哪两条线段的比例中项?请简要证明(说明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票用时,单位:分),得到如下表所示的频数分布表.
分组
频数
一组
0≤t<5
0
二组
5≤t<10
10
三组
10≤t<15
10
四组
15≤t<20
五组
20≤t<25
30
合计
100
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)旅客购票用时的平均数可能落在哪一小组内?
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么请你决策一下至少要增加几个窗口?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
相关试题

