【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() .
.

(1)如果![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 是对角线
是对角线![]() 上的点,
上的点,![]() ,则
,则![]() 的长为________;
的长为________;
(2)如果![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,
,![]() 是对角线
是对角线![]() 上的点.下列判断正确的是_____.
上的点.下列判断正确的是_____.
①在![]() 上存在无数组
上存在无数组![]() ,
,![]() ,使得四边形
,使得四边形![]() 是平行四边形;
是平行四边形;
②在![]() 上存在无数组
上存在无数组![]() ,
,![]() ,使得四边形
,使得四边形![]() 是矩形;
是矩形;
③在![]() 上存在无数组
上存在无数组![]() ,
,![]() ,使得四边形
,使得四边形![]() 是菱形;
是菱形;
④当![]() 时,存在
时,存在![]() 、
、![]() 、
、![]() ,使得四边形
,使得四边形![]() 是正方形.
是正方形.
参考答案:
【答案】2或8 ①②③④
【解析】
(1)分两种情况,点G在线段OA或OC上,首先利用矩形的性质证明![]() ,得到
,得到![]() ,然后利用直角三角形斜边中线的性质得出
,然后利用直角三角形斜边中线的性质得出![]() ,然后利用勾股定理求出AC的长度,进而可得到AO的长度,最后利用
,然后利用勾股定理求出AC的长度,进而可得到AO的长度,最后利用![]() 即可求解.
即可求解.
(2)①利用平行四边形的判定方法判定即可;
②利用矩形的判定方法判定即可;
③利用菱形的判定方法判定即可;
④先假设存在这样的正方形,然后利用正方形的性质求出AE的长度,看是否能找到满足条件的E,F,H点,进而可得出结论.
(1)当点G在线段OC上时,如图,
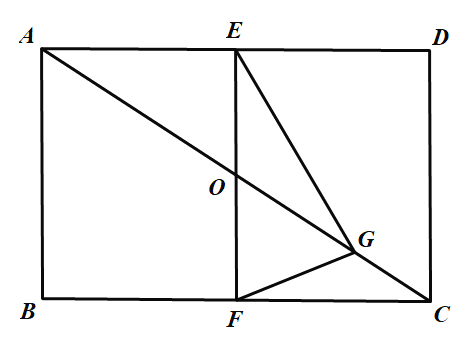
∵四边形ABCD是矩形,
∴![]() ,
,
![]() .
.
∵点E,F分别是AD,BC的中点,
∴![]() .
.
在![]() 和
和![]() 中,
中,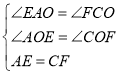
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
当点G在线段OA上时,如图,
同理可求![]() ,
,
∴![]() ,
,
综上所述,AG的长度为2或8;
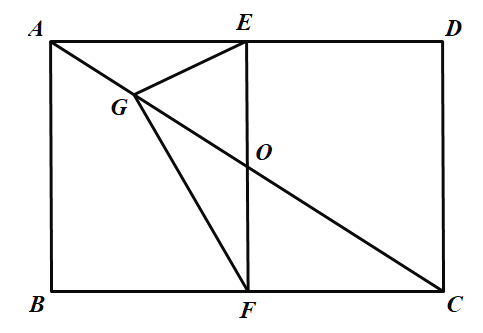
(2)只要满足![]() 即可得出四边形
即可得出四边形![]() 是平行四边形,故①正确
是平行四边形,故①正确
理由如下:
∵四边形ABCD是矩形,
∴![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,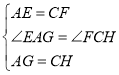
![]() ,
,
![]() ,
,
![]()
![]()
∴四边形![]() 是平行四边形;
是平行四边形;
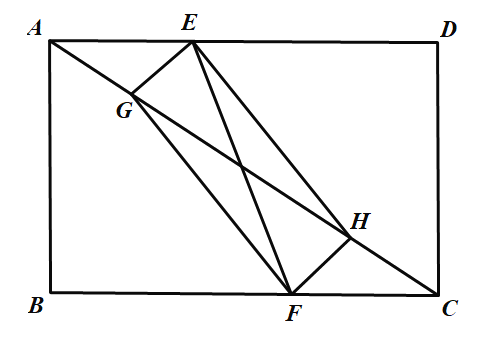
②在①的基础上再保证![]() 即可证明四边形
即可证明四边形![]() 是矩形,而满足条件的
是矩形,而满足条件的![]() 有无数个,故②正确;
有无数个,故②正确;
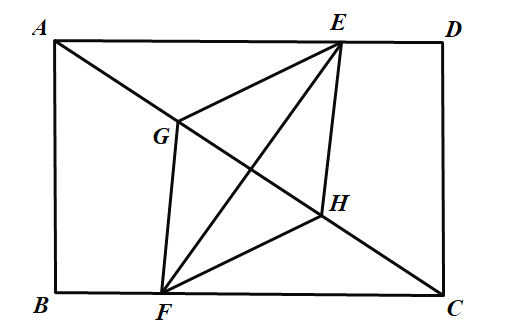
③在①的基础上,需要再满足![]() ,这时E,F点的位置就固定下来了,但是只要满足
,这时E,F点的位置就固定下来了,但是只要满足![]() 即可得到四边形
即可得到四边形![]() 是菱形,而满足条件的
是菱形,而满足条件的![]() 有无数个,故③正确;
有无数个,故③正确;
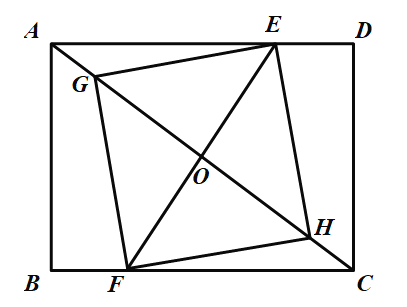
④假设当![]() 时,存在
时,存在![]() 、
、![]() 、
、![]() ,使得四边形
,使得四边形![]() 是正方形,则有
是正方形,则有![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
∴线段AD上存在点E,
∴只要同时满足![]() 就能得到四边形
就能得到四边形![]() 是正方形,故④正确.
是正方形,故④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:一张矩形纸片
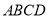 ,
,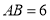 ,
,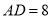 ,
,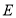 为
为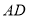 边上一动点,将矩形沿
边上一动点,将矩形沿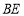 折叠,要使点
折叠,要使点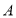 落在
落在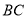 上,则折痕
上,则折痕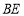 的长度是________;若点
的长度是________;若点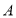 落在
落在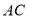 上,则折痕
上,则折痕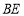 与
与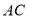 的位置关系是__________.若翻折后
的位置关系是__________.若翻折后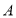 点的对应点是
点的对应点是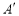 点,连接
点,连接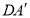 ,则在点
,则在点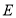 运动的过程中,
运动的过程中,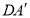 的最小值是______.
的最小值是______.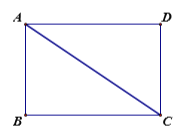
-
科目: 来源: 题型:
查看答案和解析>>【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨
频数
频率
2≤x<3
4
0.08
3≤x<4
a
b
4≤x<5
14
0.28
5≤x<6
9
c
6≤x<7
6
0.12
7≤x<8
5
0.1
合计
d
1.00

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列网格中的六边形
 是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为___________;
(2)如图甲,把六边形
 沿
沿 ,
, 剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;
剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;
(3)在图乙中画出一种与图甲不同位置的两条剪裁线,并画出将此六边形剪拼成的正方形.(通过平移,旋转,翻折与图甲重合的方法不可以)


-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求证:AB⊥BD;
(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;
(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)

相关试题

