【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
参考答案:
【答案】(1)1辆大货车和1辆小货车一次可以分别运货5吨、3吨;(2)至少需要安排3辆大货车;(3)方案1:租用4辆大货车,1辆小货车;方案2:租用1辆大货车,6辆小货车;最少租金为1400元.
【解析】
(1)设1辆大货车和1辆小货车一次可以分别运货x吨、y吨,根据“3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨”列方程组求解可得;
(2)设安排m辆大货车,则小货车需要(10-m)辆,根据两种货车运送的货物总质量不低于35吨列一元一次不等式求解可得;
(3)设租大货车a辆,小货车b辆.根据日前有23吨货物需要运输列出不等式,结合a,b为非负整数求出a,b的值,再求出各方案所需资金,比较后即可得出结论.
解:(1)设1辆大货车和1辆小货车一次可以分别运货x吨、y吨,
根据题意,得:![]() ,
,
解得:![]() ,
,
答:1辆大货车和1辆小货车一次可以分别运货5吨、3吨.
(2)设安排m辆大货车,则小货车需要(10-m)辆,
根据题意,得:5m+3(10-m)≥35,
解得:m≥2.5,
所以至少需要安排3辆大货车;
(3)设租大货车a辆,小货车b辆,由题意得
5a+3b=23,
∵a,b为非负整数,
∴![]() 或
或![]() ,
,
∴共有2中运输方案,方案1:租用4辆大货车,1辆小货车;方案2:租用1辆大货车,6辆小货车.
方案1的租金:300×4+200=1400元,
方案2的租金:300+200×6=1500元,
∵1400<1500,
∴最少租金为1400元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, .
.
(1)如果
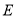 、
、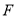 分别是
分别是 、
、 的中点,
的中点, 是对角线
是对角线 上的点,
上的点, ,则
,则 的长为________;
的长为________;(2)如果
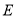 、
、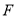 分别是
分别是 、
、 上的点,
上的点, ,
, 是对角线
是对角线 上的点.下列判断正确的是_____.
上的点.下列判断正确的是_____.①在
 上存在无数组
上存在无数组 ,
, ,使得四边形
,使得四边形 是平行四边形;
是平行四边形;②在
 上存在无数组
上存在无数组 ,
, ,使得四边形
,使得四边形 是矩形;
是矩形;③在
 上存在无数组
上存在无数组 ,
, ,使得四边形
,使得四边形 是菱形;
是菱形;④当
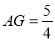 时,存在
时,存在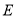 、
、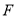 、
、 ,使得四边形
,使得四边形 是正方形.
是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列网格中的六边形
 是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为___________;
(2)如图甲,把六边形
 沿
沿 ,
, 剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;
剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;
(3)在图乙中画出一种与图甲不同位置的两条剪裁线,并画出将此六边形剪拼成的正方形.(通过平移,旋转,翻折与图甲重合的方法不可以)


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求证:AB⊥BD;
(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;
(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=
 AB.
AB.(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学完二次根式一章后,小易同学看到这样一题:“函数
 中,自变量
中,自变量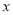 的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量
的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量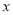 的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:第一步:函数
 中,自变量
中,自变量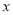 的取值范围是_____________.
的取值范围是_____________.第二步:根据自变量取值范围列表:
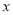
-1
0
1
2
3
4

0
1


2

 __________.
__________.第三步:描点画出函数图象.
在描点的时候,遇到了
 ,
, 这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
你能否从中得到启发,在下面的
 轴上标出表示
轴上标出表示 、
、 、
、 的点,并画出
的点,并画出 的函数图象.
的函数图象.
第四步:分析函数的性质.
请写出你发现的函数的性质(至少写两条):
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步:利用函数
 图象解含二次根式的方程和不等式.
图象解含二次根式的方程和不等式.(1)请在上面坐标系中画出
 的图象,并估算方程
的图象,并估算方程 的解.
的解.(2)不等式
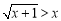 的解是__________________.
的解是__________________.
相关试题

