搜索
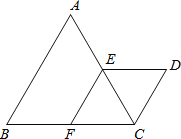
【题目】如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点。
（1） 求证：四边形EFCD是菱形；（2）如果AB=10，求D、F两点间的距离。
参考答案：
【答案】（1）证明见解析（2）
【解析】
试题分析：（1）利用三角形的中位线定理即可得到四边形EFCD的四边相等，即可证得；
（2）连接DF，与EC相交于点G，△EFC是等边三角形，则△EFG是直角三角形，利用三角函数即可求得GF的长，根据DF=2GF即可求得．
试题解析：（1）∵△ABC与△CDE都是等边三角形
∴ AB=AC=BC，ED=DC=EC
∵ 点E、F分别为AC、BC的中点
∴EF= 
，EC= 
, FC=
∴EF=EC=FC
∴EF=FC=ED=DC，
∴四边形EFCD是菱形．
（2）连接DF，与EC相交于点G，
∵四边形EFCD是菱形
∴DF⊥EC，FD=2FG
∵EF= =5, EG=
EC=
,
由勾股定理得：FG=
，则FD=
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如表所示
A
B
进价（万元/套）
1.5
1.2
售价（万元/套）
1.65
1.4
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元．
（1）该商场计划购进A，B两种品牌的教学设备各多少套？
（2）通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少的数量的1.5倍．若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知a、b满足
，
，且有理数a、b、c在数轴上对应的点分别为A、B、C．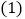
则
______，
______，
______．
点D是数轴上A点右侧一动点，点E、点F分别为CD、AD中点，当点D运动时，线段EF的长度是否发生变化，若变化，请说明理由，若不变，请求出其值；
若点A、B、C在数轴上运动，其中点C以每秒1个单位的速度向左运动，同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动
请问：是否存在一个常数m使得
不随运动时间t的改变而改变若存在，请求出m和这个不变化的值；若不存在，请说明理由．
-
科目： 来源： 题型：
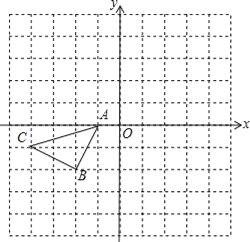
查看答案和解析>>【题目】如图的正方形格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
（1）将△ABC沿x轴翻折后再沿x轴向右平移1个单位，在图中画出平移后的△AB1C1．若△ABC内有一点P（a，b），则经过两次变换后点P的坐标变为 ．
（2）作出△ABC关于坐标原点O成中心对称的△A2B2C2．
（3）若将△ABC绕某点逆时针旋转90°后，其对应点分别为A3（2，1），B3（4，0），C3（3，﹣2），则旋转中心坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=AC，CG⊥BA交BA的延长线于点G．一等腰直角三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一条直角边与AC边在一条直线上，另一条直角边恰好经过点B．
（1）在图1中请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想；
（2）当三角尺沿AC方向平移到图2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE+DF与CG之间满足的数量关系，然后证明你的猜想；
（3）当三角尺在（2）的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，若AG：AB=5：13，BC=4
，求DE+DF的值． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在直角坐标系中。
（1）请写出△ABC各点的坐标；
（2）求出△ABC的面积S△ABC；
（3）若把△ABC向上平移2个单位，再向右平移2个单位得△A1B1C1，在图中画出△A1B1C1，并写出△A1B1C1的坐标。
-
科目： 来源： 题型：
查看答案和解析>>【题目】解不等式组．
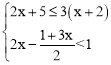把不等式组的解集在数轴上表示出来，并写出不等式组的非负整数解．
相关试题
